A synthetic approach to weathering degree classification of stone relics case study of the Yungang Grottoes

Abstract

Classification of the weathering degree of large outdoor stone relics has long been a challenge in their protection engineering. An approach to classifying the weathering levels of the Yungang Grottoes is presented in this paper. This approach is based on combined terahertz (THz) spectra and ultrasonic velocity and the use of a least squares support vector machine (LS-SVM). A regression model for prediction of the weathering level was established using the optimal values of parameters determined by the double cross-validation (D-CV) method. This SVM regression prediction model (SVMRPM) predicts the weathering levels of the grottoes with relative errors of 8.16% or less. The SVMRPM can also be used to predict the weathering levels of some areas where ultrasonic testing is extremely difficult; the THz spectra can easily be obtained using approximately 0.2 g of sample material. This method is a highly efficient and economical technique for determining the degree of weathering of large exposed stone relics.

Background

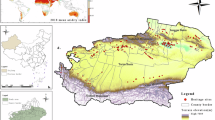
Stone relics are essential material wealth created by our ancestors. They are precious legacies with historical, artistic, and scientific value. The weathering degree of large exposed stone relics, such as the Yungang Grottoes, is an important indicator for their preservation and a significant parameter that should be determined before the relics are restored [1]. The Yungang Grottoes (Fig. 1), a world tangible heritage site located at the city of Datong in Shanxi Province of China (40°04′N, 113°20′E), consist of 53 Buddhist grottoes (Fig. 1a) and more than 51,000 statues that are noted for their collection of Buddhist grotto sculptures and reliefs from the 5th and 6th centuries. The Yungang Grottoes have been seriously damaged by the long-term adverse effects of natural forces, human influences, and environmental erosion, which pose direct threats to their existence and artistic value and also to the symbiotic social and economic benefits that they provide. Thus, it is necessary to study the weathering degree of the Yungang Grottoes. An accurate representation of the global and local weathering degree of the Yungang Grottoes is especially important for planning restoration work [2]. The methods that are commonly used to measure weathering include electrical, impact echo, Schmidt rebound, penetration-obstruction, hardness tester, and ultrasonic methods [3,4,5,6,7,8,9,10,11,12]. No one technique can be sufficient. Although these methods can be used to determine the weathering degree of rocks, they are limited in that they require numerous field tests to determine global weathering degree and may result in unnecessary damage to research objects. In addition, it is difficult to measure the weathering degree of small areas with those methods. Therefore, it is necessary to explore and design a quick, nondestructive, low-cost method for weathering degree testing and classification, which can been used as valuable reference for the restoration and protection of relics [7].

Fig. 1

Elevation and the portions of the Yungang Grottoes photographs: a elevation of Yungang Grottoes, b aerial view of Yungang Grottoes from Google Earth, and c panoramic photograph from No. 8 grotto to No. 19 grotto and the ultrasonic testing area of the external wall of No. 20 grotto, No. 19 grotto and No. 13 grotto

The weathered rocks on the external walls of the Yungang Grottoes, which are typically exposed stone relics, were evaluated in this study. First, the weathered zones on the external walls of the grottoes (Fig. 1c) were tested using a nondestructive ultrasonic machine, and the corresponding ultrasonic velocities were calculated. It has been referenced from the Engineering Geologic Mapping Committee of the International Engineering Geology Association and the Laboratory and Site Standard Committee of the International Rock Mechanics Association [13], the longitudinal ultrasonic velocity ratios of the weathered and fresh rocks represent the weathering levels of rocks in the Yungang Grottoes, as well as the classification of the weathering degrees for materials such as marble and granite [14,15,16]. Next, the terahertz (THz) spectra of the weathering samples in the study area were measured using a terahertz time-domain spectrum system (THz-TDS). This is a non-destructive, non-ionizing, high-sensitivity spectral system for synchronous coherent detection using samples weighing only approximately 0.2 g [17,18,19,20]. The THz spectral data and the corresponding weathering levels determined by means of the ultrasonic tests were combined as training and test samples. Last, a regression model for prediction of the weathering levels of the grotto walls was established based on these samples using a least squares support vector machine (LS-SVM). The LS-SVM employs a machine learning software package known for its quick operation, strong generalization, and ability to solve various practical problems, such as those involving small sample sizes, over-fitting, and high dimensions [21,22,23]. The LS-SVM regression model obtained as described above is a new, highly accurate, and economical method for predicting the weathering levels of stone relics based on experimental spectral data from weathered materials.

Materials and methods

Ultrasonic testing

According to the distribution characteristics of the weathering damage in the external walls of the Yungang Grottoes, most of the cross sections are rectangular and square. Thus, grid-based ultrasonic testing, which is commonly used in preserving cultural relics, was used to measure the weathering layers of the external walls of the Yungang Grottoes (Fig. 1c). The “fixed excitation probe and moving receive probe” and “synchronous movement of excitation and receive probes” methods were used separately. Each test area consisted of at least three survey lines, and every survey line had at least six measured points. The horizontal and vertical distances between adjacent measuring points were 5 cm. The measured results were recorded according to the grotto number of the test area. For example, the ultrasonic testing results for the No. 20 grotto were recorded using the code number 20. Similarly, the THz spectral measurements were recorded according to the grotto number of each sampling site.

A wide-band sonic detector was used for ultrasonic testing. The excitation transducer used a 50-kHz excitation probe. The emission voltage, transmission gain, number of sampling points, and sampling interval were set to 250 V, 36 dB, 2000, and 1 s, respectively. In addition, to reduce the air space between the emission probe (or the receiving probe) and the outer walls of the grottoes and to increase the detection sensitivity, normal glue was chosen as the coupling agent. The normal glue is boiled from wheat flour and water at a 1:6 ration under 353 K, which is availability, suitability for direct use, and quasi-flow structure. Normal glue does not penetrate easily into stones, it does not cause secondary pollution, and it is easy to clean. Considering the unevenness of the testing regions, uneven coating of the coupling agent and variation in the placement of transducers during field ultrasonic, there may be some errors in the test results. Outliers in the original ultrasonic wave time (t) data are eliminated before the data analysis using Grubbs’ test. By looking up Grubbs’ tables, we are able to obtain values of G (n₀) for use in excluding outliers [for which G is greater than G (n₀)]. And G is defined as follows:

$${\text{G}} = \left| {\frac{{\overline{\text{t}} - {\text{t}}_{\text{n}} }}{\text{s}}} \right| = \left| {\frac{{\frac{1}{\text{n}}\mathop \sum \nolimits_{{{\text{i}} = 1}}^{\text{n}} {\text{t}}_{\text{i}} - {\text{t}}_{\text{n}} }}{{\sqrt {\frac{1}{{{\text{n}} - 1}}\mathop \sum \nolimits_{{{\text{i}} = 1}}^{\text{n}} \left( {{\text{t}}_{\text{i}} - \frac{1}{\text{n}}\mathop \sum \nolimits_{{{\text{i}} = 1}}^{\text{n}} {\text{t}}_{\text{i}} } \right)^{2} } }}} \right|$$

(1)

where $\overline{\text{t}}$ is the average of all ultrasonic wave time (t) data, s is the standard deviation, and n₀ is the significance level, which was taken to be 5%.

The longitudinal ultrasonic velocity (V) of each grid unit of the tested grotto walls are calculated using the t measured by the mobile ultrasonoscope and the mesh scale within the corresponding transmit–receive intervals.

THz spectral measurement

Sample preparation

To minimize damage to the relics, three small weathering samples were collected from the ultrasonic testing regions (Fig. 1c) and then ground evenly with an agate mortar. Each powder sample was marked according to the grotto number. To reduce the scattering effect of the test sample, 0.1 g of a standard ground sample was mixed with 0.1 g of polyethylene powder (1:1) and then sieved by filtering with 200-eye sieves. Each sample was then compressed into a round tablet (diameter: 1.3 cm; thickness: approximately 1 mm) with smooth parallel surfaces used an infrared tablet under a pressure of 5 tons.

Experimental setup

The spectral data of the weathered samples were collected by transient THz-TDS [24]. A titanium sapphire femtosecond pulsed laser was used to generate laser light sources with a 800-nm central wavelength, 80-MHz repetition frequency, 100-fs pulse width, and 960-mW power output. A p-InAs crystal was used to excite the THz electromagnetic impulse, and a ZnTe crystal was used as the detection crystal. The samples were placed on the focal point between two parabolic mirrors. The setup was placed in a chamber filled with N₂ to eliminate the influence of water vapor in the air. The relative humidity was less than 4%, and the temperature was 293 K.

The experimental data conformed to the physical model developed by Dorney and Duvillaret for extraction of the THz optical parameters of materials [25, 26]. THz-TDS can be used to measure the time-domain waveform of the reference and sample signals and then obtain the corresponding frequency-domain spectra using a fast Fourier transform. By comparing the sample and reference pulses, the complex transmissivity (T) can be defined as follows:

$$T\left( \omega \right) = \left| {\frac{{A_{{{\text{sample}}\left( \omega \right)}} }}{{A_{{{\text{reference}}\left( \omega \right)}} }}} \right|^{2} = \left| {t_{N} (\omega )} \right|^{2} \exp \left[ {\varphi_{N} \left( \omega \right)} \right]$$

(2)

where A_reference is the complex amplitude of the reference, A_sample is the complex amplitude of the sample, N is the complex refractive index of the sample, ω is the frequency of radiation, |t_N(ω)| is the transmission coefficient, and $\varphi_{N} ( \omega )$ is the related phase difference between the reference and sample spectra.

LS-SVM

Due to its non-linear algorithm, the SVM is particularly adapted to separating samples with similar profiles. And the key to LS-SVM modelling is the selection of the kernel function and its parameters, which have a direct influence on the prediction accuracy. After contrasting kernel functions in the SVM, a radial basis function (RBF) was chosen to train the SVM in this study [27, 28]. The RBF is a nonlinear function that reduces the complexity of computation during training. Different parameters have to be optimized to increase the performance of the algorithm, like the three parameters are a penalty factor (c), an insensitivity loss parameter (ε), and an RBF coefficient (γ). The corresponding effective value ranges of the three parameters were 2⁻¹⁰–2¹⁵, 2⁻¹⁰–2³, and 2⁻¹⁰–2¹⁰, respectively. The double cross-validation (D-CV) method was used to search for the optimum c, ε, and γ values. The THz spectra of the grotto walls and the regression model for predicting the degree of weathering were obtained in this manner. The prediction accuracy of the model was evaluated in terms of the relative error (RE) of the predictions.

Result and discussion

Weathering level

Before the stone relics can be repaired, the degrees of weathering of the different parts must be determined accurately. Thus, the range of degrees of weathering of the stone relics was divided into 10 levels numbered from 1 to 10, based on the longitudinal ultrasonic velocity [13, 15]. The weathering level (L_T) was defined as follows:

$${\text{L}}_{\text{T}} = 10{-}{\text{INT}}\left[ { 10 \, \times \, \left( {{\text{V}}/{\text{V}}_{0} } \right)} \right]$$

(3)

where the INT function rounds the object of the function up to the nearest integer, V is the longitudinal ultrasonic velocity of each grid unit of the tested grotto walls, and V₀ is the longitudinal ultrasonic velocity of a fresh core close to the No. 13 grotto, with properties similar to those of the other grottoes, measured to be 2963.42 m/s. The mean longitudinal ultrasonic velocities (V) of some tested grotto walls and the tested weathering levels (L_T) are listed in Table 1.

Table 1 Measurement results for some grotto walls

THz spectra

THz-TDS can be used to measure the real-time waveforms of sample signals directly. Figure 2a shows the time-domain spectra of samples from the grotto walls. The THz time-domain spectra reveal variations in the THz pulse intensity and time delay between the samples’ signals. Different propagation velocities in the samples relative to the reference path give rise to differences in the time delay, while the variation in the terahertz pulse intensity results from sample reflection and absorption, as well as the THz pulse being broadened as the sample dispersion increases. The time-domain spectra of samples can be changed into transmission spectra using a fast Fourier transform and Eq. 2. The corresponding THz transmission spectra of samples from the grotto walls are shown in Fig. 2b. Because a THz wave is sensitive to weak changes in the molecular structure, the transmission coefficients of the different samples can be detected in the terahertz band. By this means, different samples can be distinguished. However, within the testing waveband, no obvious transmission peak was observed in the samples. Therefore, a common weathering classification based on a characteristic peak is inapplicable, and a new classification method have to be developed. And in order to improve the accuracy of the effect analysis of the model, high-resolution THz spectra in the range of 0.6–1.6 THz (Fig. 2b) are chosen, and the corresponding T values are used as training and test samples for SVM modelling.

Fig. 2

THz spectra of grotto wall samples: a THz time-domain spectra of grotto wall samples, and b THz transmission spectra of grotto wall samples as training and test samples

Establishment of SVM prediction regression model

Firstly, transmittance data for the external wall samples within the 0.6–1.6 THz range (Fig. 2b) are collected from the Yungang Grottoes and taken as the input data. Secondly, the corresponding weathering levels of the samples (Table 1), which is computed by forum 1 with data sifted from Grubbs are produced as the output data. Thirdly, these data are used as a complete data set and converted into the SVM^Light format file. The data file is stored as a.TXT file and considered to be the training and testing data set (Table 2), which contain 17 samples in total, each sample has 34 variables.

Table 2 Training and testing data set

The prediction model was constructed using the preconditioned spectral data and tested against a blind test set. Subsequently, the D-CV method was chosen for determination of the adaptive parameter to avoid overfitting of the data and ensure modelling accuracy and universality. This procedure was performed 17 times with different combinations of data. The prediction model was constructed using the preconditioned spectral data and tested against a blind test set. This resulted in a true blind test with the additional challenge of spectral data. Every model variation was thus trained using 544 (16 samples × 34 variables) spectral data points, with a blind test set of 34 spectral data points. The RE of the model was used to evaluate the ability of the model to predict weathering levels. The optimal values of the three model parameters were determined to be c = 16, ε = 0.008, and γ = 2.0625. The predicted values (L_P) and RE values are listed in Table 1. The REs were all less than 8.16%, which indicates that the model is reliable and applicable to predicting weathering levels.

Application of the regression prediction model

The Yungang Grottoes, which are considered a part of world cultural heritage, cannot be replaced; thus, damage to the grottoes during testing is not allowed. Ultrasonic testing is inapplicable to most Buddha carving regions, especially the uneven statues. This limitation means that ultrasonic testing cannot be performed to measure acoustic waves and analyze the degree of weathering for fear of further damage. However, THz spectral measurement through THz-TDS requires just samples weighing only approximately 0.2 g. Some weathered carving samples as small as such could be obtained outside of the main body of the stone relics. Thereafter, the weathering levels of the regions where ultrasonic testing cannot be predicted by applying the transmittance data of the THz-TDS spectra within the 0.6–1.6 THz waveband to the SVMRPM. The transmittance data of the THz-TDS spectra should first be converted to the SVM^Light data format before they are put in the SVMRPM as sample data. The THz transmitted spectra of the grotto wall samples with unknown weathering levels used as forecast samples are shown in Fig. 3. The THz spectrum offset in different weathered grottoes samples is mainly caused by the component difference of the samples, and the THz-TDS with the sensitive characteristics for identifying material composition which can effectively distinguish samples with different levels of weathering. The prediction sample set of the transmittance data in the SVM^Light data file format is shown in Table 3. The predicted weathering levels are listed in Table 4.

Fig. 3

THz transmission spectra of grotto wall samples with unknown weathering level as forecast samples

Table 3 Forecast data set

Table 4 Weathering level prediction results

Conclusions

Previous studies on characterization of the degree of weathering of large exposed stone relics have focused mainly on experimental or test analyses, which involve sampling methods that may bring further effect on relics. These methods can only be used to test-safe zones; they cannot be applied to the main parts of such relics. In this study, a SVMRPM is developed to predict weathering levels based on THz spectra and ultrasonic experimental data. The basic principle and algorithm of SVMRPM are used to analyze and predict the weathering levels of stone relics. The prediction results show that the SVMRPM is effective in processing the spectral data despite the fact that no characteristic peak is found in the spectral data and the spectral differences among several samples are small. The SVMRPM based on THz spectral data and ultrasonic experimental data demonstrated good performance, with RE values of less than 8.16%. This would provide a new, highly efficient, and economical weathering test technique for the Yungang Grottoes. The proposed model can also be applied to analyzing the degree of weathering for other stone relics.