An evaluation system for the development of scaling off at earthen sites in arid areas in NW China

Abstract

Earthen sites are valuable cultural heritage sites in arid regions of NW China, where a series of serious deteriorations have developed. Scaling off is a typical type of deterioration that greatly threatens the long-term preservation of earthen sites. To date, there are insufficient studies on the formation mechanisms and influence factors of scaling off, leading to a lack of a theoretical foundation for further consolidation research. Therefore, establishing a scientific evaluation system to explore the formation mechanisms of scaling off and assess its degree of development has become a very significant topic for earthen site conservation. In this study, we selected 18 earthen sites to survey scaling off in the field, and data from geotechnical tests and meteorology were then collected to fit the characteristic values to determine the influencing factors. Finally, fuzzy analytic hierarchy process (Fuzzy-AHP) was applied to build a system to evaluate scaling off. The mechanisms of scaling off formation were explained by comparing and analyzing the porosity, shrinkage limit, particle size distribution of rammed earth and environmental factors combined with soluble salt contents in rammed earth. This research reveals the formation mechanisms and influencing factors of scaling off from a new perspective, which will lay a beneficial foundation for further consolidation research.

Introduction

Earthen sites distributed in the arid regions of NW China are precious cultural heritage sites with very high history, art, and science value [1]. After experiencing approximately 500 hundred years of natural erosion and human destruction, most of these sites have developed a series of typical deteriorations that threaten their long-term existence and preservation. Four modes of deterioration have occurred in Jiaohe Ancient City: winter-related deterioration, water-related deterioration, temperature-related deterioration and chemical-related deterioration [2]. The correlations between the deterioration of earthen sites and their factors were previously studied, and a model to illustrate the formation mechanisms and evolution of deteriorations of earthen sites in Qinghai Province, China, was established [3]. The types of deterioration that have developed at the earthen sites of the Ming Great Wall mainly include crazing, gully erosion, surface crust erosion, bottom sapping, and collapse [4]. Such studies have revealed the significant effects of the environment and material properties on the formation and development of those deteriorations. Specifically, as earthen sites are mainly preserved in the open air, environmental factors are the most destructive natural actions causing these deteriorations [2]. Rammed earth, which is the main building material for earthen sites, has heterogeneous physical, water-related, and mechanical properties, which are interior factors that cause the deteriorations of earthen sites [3].

Scaling off is one of the most typical types of deterioration that accelerates the degradation of earthen sites and is also an important model of the gradual extinction of earthen sites [2, 5]. Currently, the research on this type of deterioration is still in the exploratory stage, and there are few systematic studies on its formation factors. Scaling off is the result of the combined functions of water, temperature, salt, and wind [6]. Scaling off occurs because the surface soils become saturated and disintegrate under the effects of rainfall to generate slurry films, which will be subsequently detached by wind erosion and the expansion–contraction induced by the change in temperature [7]. In NW China, the categories of scaling off for different rain-erosion and wind-erosion types have been defined based on momentum differences [8]. Although the initial formation of scaling off can protect earthen sites from weathering, it accelerates the deterioration process due to the rapid peeling and falling off in later development stages. Thus, the formation mechanism of scaling off is a very complex process. So far, the research on the formation mechanisms of scaling off is not comprehensive or deep enough, leading to the difficulty in consolidation work. For instance, permeation methods were utilized by applying traditional chemical grouts to materials undergoing scaling off; however, the consolidation effects from these methods were not ideal, and the new method of biological reinforcement using mosses still needs to be verified further. Therefore, it is essential to research the formation mechanisms and evaluation systems from the perspectives of the occurrence environment and building materials to provide a theoretical basis for consolidation aimed at scaling off.

In this research, the authors selected 18 typical earthen sites located in the arid regions in NW China as the study objects. By surveying the scaling off at these sites in the field and collecting the rammed earth samples from each corresponding site, the characteristic values of scaling off were determined. After collecting meteorological data and performing related geotechnical experiments, the authors fitted scaling off characteristic values with the engineering properties of rammed earth and environmental factors to explore the factors that influence scaling off. Furthermore, the fuzzy analytic hierarchy process (Fuzzy-AHP) was applied to build a system to evaluate scaling off and calculate its degree of development at each site, which is a scientific evaluation method combined with objective and subjective aspects. By comparing and analyzing the porosity, shrinkage limit, particle size distribution of rammed earth and environmental reasons combined with soluble salt contained in crusted and loose layers, the formation mechanisms of scaling off are explained. This research proposes a new formation mechanism and evaluation system, which will lay the foundation for the further consolidation and preservation of earthen sites in NW China.

Study area

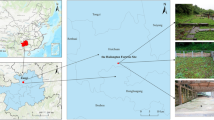
In NW China, there are many earthen sites of the Ming Great Wall, which were built according to the local conditions and materials via plate-building technology. The main material used for these earthen sites was rammed earth, which is a type of manufactured material containing sand, gravel, and clay [9]. To ensure representativeness, objectivity, and consistency of the earthen sites studied in this research, all sites should be located in the same areas, constructed in the same times, and built by similar techniques. Therefore, the authors selected 18 earthen sites that are distributed in extremely arid regions, semiarid regions and arid regions in Qinghai and Gansu Provinces, NW China (Table 1). Among these sites, 4 earthen sites are located in extremely arid regions, 3 sites are located in semiarid regions, and 11 sites are located in arid regions. Rammed earth samples were collected from each site to perform related geotechnical experiments. To follow the minimum damage principle, the authors collected as few samples as possible when the conditions were not rainy. The study area and related earthen sites are shown in Fig. 1.

Table 1 The location, meteorological data and geographical coordinates of earthen sites selected in this research

Fig. 1

The study area in this research

Methods

In this research, the authors surveyed scaling off to determine characteristic values and collected related data on site. Then, rammed earth samples from each site were collected to perform geotechnical tests to obtain data on the engineering properties of the rammed earth. Meteorological data were also obtained from the local meteorological bureaus. By fitting these data, the influencing factors that caused scaling off were finally determined. After that, the Fuzzy-AHP was applied to establish a system to evaluate the scaling off at earthen sites by calculating the degree of scaling off development.

Field investigations

In this research, the authors surveyed 18 earthen sites in the field to investigate and collect deterioration data in accordance with the Specifications of Investigation for Preservation Engineering of Earthen Sites (WW/T 0040-2012), issued by the State Administration of Cultural Heritage of the People’s Republic of China [10]. Different degrees of scaling off existed at all sites, and this type of deterioration was distributed from the top to the bottom sapping areas of earthen walls. Scaling off areas were cut by cracks to become trapezoids, and some of these trapezoids had lifted edges, causing them to fall out.

To collect the data that accurately reflected the development of scaling off, the plane and profile characteristics were investigated in the field. Then, the characteristic values were determined on the basis of the investigation outcomes to show the degree of scaling off development.

Plane Characteristics: To obtain a quantitative index to characterize the plane morphological features of scaling off, the authors mainly selected a 1 m² area of the wall at each site as a statistical unit. In this area, only scaling off was present, while other types of deterioration had not developed. This method mainly is referred to as the statistical window method in geology. Then, we used a digital camera to capture an image of the 1 m² area of the selected wall, and we processed this image by applying AutoCAD. For example, as shown in Fig. 2, within the 1 m² area of the statistical unit surrounded by the yellow line, there are 26 scaling offs that are divided by the red fracture lines. We calculated the area of each scaling off using AutoCAD and then calculated the average area of all scaling offs within this statistical unit. This average area is defined as the advantage area of scaling off. Using this sampling method, the advantage areas of the scaling off in the extremely arid, arid and semiarid regions are 125–150 cm², 85–115 cm², and 55–75 cm², respectively.

Fig. 2

A statistical unit of scaling off developed on an earthen wall

Profile characteristics

To reveal the degree of longitudinal development of scaling off, the authors selected 5 scaling off regions from the top to the bottom of the wall at each earthen site. The soil on the surface was cut, which revealed an obvious stratification phenomenon (Fig. 3). The surface soil that has been apparently broken away from its underlying soil is defined as the first soil layer. On the trailing edge of the first soil layer, cracks parallel to the wall are developed. After removing the first soil layer, the second soil layer was found to have loose soil structures with a large amount of white crystalline substances aggregated on the surface of the second soil layer. The authors removed the second soil layer until dense soil structures were reached, which was defined as the third soil layer. The soil in this layer belongs to the primary rammed earth of earthen sites. Compared to the other two layers, the third soil layer was scratched when a knife was used to carve its surface, but the layer did not peel off. By measuring the thicknesses of the first two soil layers at each site with a digital caliper, the average thickness of each soil layer of all earthen sites could be obtained. The results show that the thickness of the first soil layer ranged from 9.1 to 17.56 mm, while the second soil layer ranged from 21.75 to 45.85 mm. These two soil layers have also been called crusted layers and loose layers [2]. Here, the authors defined scaling off as a characteristic binary structure including the crusted layer and loose layer.

Fig. 3

The profile of scaling off

From the results of the field investigations on the plane and profile characteristics of scaling off, the authors determined that three characteristic values of scaling off can be used to determine the degree of development, namely, advantage area, the thickness of the crusted layer and thickness of the loose layer. The data on the characteristic values of scaling off at 18 earthen sites are listed in Table 2.

Table 2 The data on characteristic values of scaling off at 18 earthen sites

Geotechnical tests

To gain the related engineering properties of rammed earth, the authors sampled the rammed earth of each earthen site and performed geotechnical tests to measure the grain size, porosity and shrinkage limit of the samples in accordance with the Testing Techniques Specification for Preservation of Earthen Sites (WW/T 0039-2012) issued by the State Administration of Cultural Heritage of the People’s Republic of China [11], shown in Table 3.

Table 3 The indices of engineering properties of rammed earth determined by the related geotechnical tests

Grain size test

A rammed earth sample was collected from each the first, second and third soil layers in the scaling off regions at each corresponding earthen site. These samples were fully crushed, evenly mixed, and 200 g was sampled using the quartation method. Sieve analysis and hydrometer methods were then used. Specifically, the sieve analysis method was applied to measure the sizes of coarse grains (over 0.075 mm), while the hydrometer method was suitable to measure the sizes of fine grains (under 0.075 mm). Through conducting grain size tests, the clay and silt particle contents were acquired, shown in Table 3.

Porosity test

As the crusted layer is thin and the soil on the loose layer is brittle, it is difficult to use the cutting ring method. For this reason, the wax-coated method was chosen to measure the porosity, shown in Table 3. Based on the principle of Archimedes, the volume of soil was measured by using the density ratio of pure water at the same temperature.

Shrinkage limit test

After the rammed earth samples were completely dried, they were fully mixed with distilled water with a liquid limit that was 1.5 times as much as the samples to create paste solutions that were initially saturated. The samples were left to stand for more than 1 day to prevent the formation of aggregate structures; then, the liquid paraffin method was applied to measure the shrinkage limits of the samples [12].

Meteorological data

Meteorological data from 18 earthen sites were also collected from the local weather bureaus, including annual rainfall, annual evaporation, and average annual temperature diurnal ranges, as listed in Table 1.

After obtaining all the geotechnical and meteorology data, the authors fit these data to the previously measured characteristic values to explore the factors that influenced scaling off.

Fuzzy-AHP

The AHP is a flexible method to resolve complex decisions based on comparisons of individual judgments [13, 14]. This method has been widely used since it easily handles multiple criteria and can also effectively process both qualitative and quantitative data [15]. However, this method has some drawbacks. For example, this method cannot reflect the style of human thoughts, and it is subjective and imprecise [16]. Fuzzy set theory was combined with the AHP to solve this problem [17], which is called the Fuzzy-AHP. This approach is an appropriate and efficient method for complex decisions in environmental and municipal management [14].

Considering the particularity of cultural heritage, especially for the Great Wall, which is a significant part of world-class cultural heritage with historical, artistic and scientific values, it is very important to consider expert opinions when studying the deterioration mechanisms and protective measures. In this research, we selected Fuzzy-AHP because it can reflect the subjective intentions of the decision maker, provide the hierarchical structure, facilitate decomposition and pairwise comparison, reduce inconsistencies and generate priority vectors. To date, this method has been used in a wide variety of fields, including the assessment of landslide hazards, the selection of government-sponsored projects, the assessment of environmental impacts, hazard assessments at the Mogao Grottoes, China, and the assessment of seismic hazards in hydraulic fracture areas [18,19,20,21,22].

Due to the advantage of its combination of subjectivity and objectivity, Fuzzy-AHP was selected to establish a system for evaluating scaling off to calculate its degree of development at each site. The flowchart of the implementation process of the algorithm, including the coupling of AHP and the fuzzy algorithm, is illustrated in Fig. 4.

Fig. 4

Flowchart of the implementation process of the algorithm

The specific procedures of this method are as follows:

• Step 1: The hierarchical structure of the development of scaling off is established on the basis of the fitting results.

• Step 2: The weights of the indices in the hierarchical structure are obtained using the AHP. In accordance with the expert opinions, the elements of a particular layer are compared pairwise with respect to a specific element in the above layer. The weight decision matrix A can be given as follows:

  $$A = \left( {a_{ij} } \right)_{{{\text{n}} \times {\text{n}}}} \left( {n{\text{ is the number of elements compared}}} \right)$$

  (1)

  where a_ij is governed by the rules: a_ij > 0; a_ij = 1/a_ji (i ≠ j); a_ij= 1 (i = j=1,2,…,n).

  a_ij indicates a quantified judgment on a pair of elements A_i and A_j, which indicate sets of elements. The value of a_ij was determined from a 9-point scale, indicating preferences between options as equally, moderately, strongly, very strongly, and extremely preferred. These preferences can be expressed as pairwise weights of 1, 3, 5, 7 and 9, while 2, 4, 6, and 8 are intermediate values [23]. Then, the consistency index (CI) can be applied to ensure that each pairwise comparison is consistent with others. The random index (RI) and its values for different scales of matrices are listed in Table 4 [24].

  The weight of an index and the largest eigenvalue of matrix A can be calculated according to the eigenvector approach [13], as shown in Eq. (2):

  $$Aw = \lambda_{\text{max} } w \,$$

  (2)

  where w = [w₁, w₂, …, w_n] is the vector of weights, A is the weight decision matrix, and λ_max is the largest eigenvalue of matrix A. Here, the authors used the eigenvector function in MATLAB to calculate w and λ_max.

  The CI was calculated by Eq. (3):

  $$CI = \left( {\lambda_{\text{max} } - n} \right)/\left( {n - 1} \right)$$

  (3)

  The judgmental consistency of matrix A can be obtained by calculating the consistency ratio (CR):

  $$CR = \frac{CI}{RI}$$

  (4)

  When CR ≤ 0.1, the matrix can be regarded as consistent.

• Step 3: The evaluation criteria and data normalization were determined. The evaluation criteria were defined as follows:

  $$V = \left\{ {v_{1} ,v_{2} , \ldots ,v_{q} } \right\}$$

  (5)

  where q is the number of levels. Here, we defined the degrees of scaling off development as 4 levels: very high (v₁), high (v₂), moderate (v₃), low (v₄). The corresponding scores are as follows:

  $$\left. \begin{aligned} v_{1} & = [0.75,1.0] \\ v_{2} & = [0.5,0.75) \\ v_{3} & = [0.25,0.5) \\ v_{4} & = [0,0.25] \\ \end{aligned} \right\}$$

  (6)

  The decision matrix C was defined in Eq. (7):

  $$C = \left[ {\begin{array}{*{20}c} {X_{11} } & {X_{12} } & \cdots & {X_{1k} } \\ {X_{21} } & {X_{22} } & \cdots & {X_{2k} } \\ \vdots & \vdots & \ddots & \vdots \\ {X_{l1} } & {X_{l2} } & \cdots & {X_{lk} } \\ \end{array} } \right]$$

  (7)

  which contains ‘k’ indices in the index layer and ‘l’ alternatives. In Eq. (7), X_ij is the jth evaluation index of the ith alternative; l is the number of alternatives, and k is the number of indices.

  All data in matrix C need to be normalized to form the normalized decision matrix E:

  $$E = (e_{ij} )_{l \times k}$$

  (8)

  For positive elements of indices:

  $$e_{ij} = \frac{{X_{ij} - \min_{j} (X_{ij} )}}{{\max_{j} (X_{ij} ) - \min_{j} (X_{ij} )}}$$

  (9)

  For negative elements of indices:

  $$e_{ij} = \frac{{\max_{j} (X_{ij} ) - X_{ij} }}{{\max_{j} (X_{ij} ) - \min_{j} (X_{ij} )}}$$

  (10)

• Step 4: The relative membership was determined using fuzzy set theory as follows:

  $$R = \left[ {\begin{array}{*{20}c} {R_{1} } \\ {R_{2} } \\ \vdots \\ {R_{p} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\text{r}}_{11} } & {r_{12} } & \cdots & {r_{1q} } \\ {r_{21} } & {r_{22} } & \cdots & {r_{2q} } \\ \vdots & \vdots & \ddots & \vdots \\ {r_{p1} } & {r_{p2} } & \cdots & {r_{pq} } \\ \end{array} } \right]$$

  (11)

  where R indicates the membership of the ith index belonging to the jth rank, p is the number of factors within the criterion layer, and q is the number of levels. The membership function is established according to the characteristics of the index system. Specifically, we defined the degrees of scaling off development as 4 levels, as shown in Eq. (6). The triangular membership function in this research is selected and established based on that definition. In this study, the triangular membership function was used to structure the fuzzy set, as shown in Eq. (12):

  $$\left. \begin{aligned} r_{p1} = \left\{ {\begin{array}{*{20}c} 1 \quad & { \, e \ge 0.875} \\ {\frac{e - 0.625}{0.25}} \quad & {0.625 < e < 0.875} \\ 0 \quad & { \, e < 0.625} \\ \end{array} } \right. \hfill \\ r_{p2} = \left\{ {\begin{array}{*{20}c} 0 \quad & {e \ge 0.875} \\ {\frac{0.875 - e}{0.25}} \quad & {0.625 \le e < 0.875} \\ {\frac{e - 0.375}{0.25}} \quad & {0.375 \le e < 0.625} \\ 0 \quad & {e < 0.375} \\ \end{array} } \right. \hfill \\ r_{p3} = \left\{ {\begin{array}{*{20}c} 0 \quad & {e \ge 0.625} \\ {\frac{0.625 - e}{0.25}} \quad & {0.375 \le e < 0.625} \\ {\frac{e - 0.125}{0.25}} \quad & {0.125 \le e < 0.375} \\ 0 \quad & {e < 0.125} \\ \end{array} } \right. \hfill \\ r_{p4} = \left\{ {\begin{array}{*{20}c} 1 \quad & {e < 0.125} \\ {\frac{0.375 - e}{0.25}} \quad & {0.125 \le e < 0.375} \\ 0 \quad & {e \ge 0.375} \\ \end{array} } \right. \hfill \\ \end{aligned} \right\}$$

  (12)

  where e is the normalized value of each alternative and has been mentioned in step 3. This step is the core algorithm of fuzzy evaluation.

• Step 5: The comprehensive evaluation level using Fuzzy-AHP was determined, and the comprehensive evaluation vector B_i was established:

  $$B_{i} = W_{1i} \times R_{i}$$

  (13)
  $$B = \left[ {\begin{array}{*{20}c} {B_{1} } & {B_{2} } & \cdots & {B_{p} } \\ \end{array} } \right]^{T}$$

  (14)
  $$T = W_{2i} \times B$$

  (15)

  where W_1i is the weight of the indices in the index layer, B is the criterion layer’s evaluation matrix, W_2i is the weight of the indices in the criterion layer, p is the number of factors within the criterion layer, and T is the goal layer’s comprehensive evaluation vector. Here, the multiplication signs in Eqs. (13) and (15) correspond to the weighted average operator of “point-crossing” type in the fuzzy algorithm.

Table 4 The random index (RI) values

Then, the comprehensive evaluation score of development H was calculated via the weighted mean in Eq. (16). From the criteria used to assess the degree of development, when 0 ≤ H < 0.25, the degree of scaling off development is low (L); when 0.25 ≤ H < 0.5, the degree of development is moderate (M); when 0.5 ≤ H < 0.75, the degree of development is high (H); when 0.75 ≤ H < 1, the degree of development is very high (VH).

$$H = T \times S^{T}$$

(16)

where S = [0.875, 0.625, 0.375, 0.125] are the mid-score of each degree.

By obtaining the comprehensive evaluation score, the degree of scaling off development at each site can be determined.

Results

In this part, the authors fit the results to determine the factors that influenced scaling off and then established a hierarchical structure of the development of scaling off, calculated the weights of the indices in the hierarchical structure and finally obtained the degree of scaling off development at each earthen site.

Fitting results

The data of characteristic scaling off values were fitted with the related data from the geotechnical tests on the rammed earth samples and meteorological data from 18 earthen sites. Linear and polynomial fitting methods were applied, which were the most common regression methods in geotechnical engineering and were also applied to research the correlations among the deterioration of earthen sites and their influencing factors [3]. In this study, this method was used to research the factors that influenced scaling off with the help of Origin Software by automatic fitting to process the data. According to the fitting results, the correlation coefficient (R²) can reflect the degree of influence of each factor. Furthermore, as a validation procedure, the k-fold cross-validation was applied to report validated R² values (i.e. Q²). As there are 18 groups of data in each regression analysis, k was determined to be 9 for the convenience of data processing. The Q² of the model was reported in the following regression figures.

The advantage area of scaling off was fit to the porosity and shrinkage limit of rammed earth, which revealed a negative correlation between the advantage area and porosity and a positive correlation between the advantage area and shrinkage limit (Fig. 5). Therefore, porosity and shrinkage limit influenced the development of scaling off.

Fig. 5

The correlations of scaling off advantage area with porosity and shrinkage limit of rammed earth

According to the fitting results (Fig. 6a) between the thickness of the crusted layers and the porosity and shrinkage limit of the rammed earth in these layers, there was a negative correlation between the thickness of the crusted layers and porosity, but there was a positive correlation between the thickness and shrinkage limit. These results are similar to the correlations obtained for the advantage area. In addition, the authors also found that the thickness of crusted layers is related to clay and coarse silt contents (Fig. 6b). Specifically, the thickness has a positive correlation with the clay content but a negative correlation with the coarse silt content. For the meteorological data, the thickness of crusted layers is negatively correlated with annual rainfall but positively correlated with annual evaporation (Fig. 6c).

Fig. 6

The correlations of crusted layers thickness. a Porosity and shrinkage limit; b clay and coarse silt contents; c rainfall and evaporation

The same method was also applied to explore the correlations of loose layers. As shown in Fig. 7a, the thickness of the loose layers is positively correlated with porosity and negatively correlated with the shrinkage limit of rammed earth in loose layers. Figure 7b indicates that the thickness of loose layers is positively correlated with coarse silt contents but exhibits no relationship with clay contents. The fitting results indicate that the relationships between the thickness of loose layers and meteorological data are opposite the relationships between crusted layers and meteorological data. There is a positive correlation between the thickness of loose layers and annual rainfall, while there is a negative correlation between the thickness of loose layers and annual evaporation (Fig. 7c).

Fig. 7

The correlations of loose layers thickness. a Porosity and shrinkage limit; b coarse silt contents; c rainfall and evaporation

Therefore, the factors that influenced scaling off were determined, namely, porosity, shrinkage limit, clay contents, coarse silt contents of rammed earth, rainfall and evaporation of occurrence environments.

Fuzzy-AHP

Based on the fitting results, the hierarchical structure of the development of scaling off was established, as shown in Fig. 8. The development of scaling off was defined as the goal layer. There are three characteristic values that characterize the development of scaling off, namely, advantage area and the thicknesses of the crusted and loose layers, which make up the criterion layer. The index layers include porosity, shrinkage limit, clay contents, coarse silt contents of rammed earth in the host soil layer, crusted layer and loose layer, and the rainfall and evaporation of corresponding environments. There are two reasons why the index layer has some duplications: (1) As some indices are positive elements for one characteristic value while they are negative elements for other characteristic values at the same time, they have been separated to characterize their influence on the corresponding characteristic values for the convenience of data processing. (2) For the engineering property indices, such as the porosity, shrinkage limit, clay contents, and coarse silt contents, the data are different because we collected rammed earth samples from crusted layers, loose layers and host soil layers to perform related geotechnical tests. For example, although C₁, C₃ and C₉ are all the porosity of the rammed earth, C₁ represents the porosity of the rammed earth sampled from the host soil layers, C₃ represents the porosity of the rammed earth sampled from the crusted soil layers, and C₉ represents the porosity of the rammed earth sampled from the loose soil layers.

Fig. 8

The hierarchical structure of scaling off development

Combined with the rich working experience of experts and the previously obtained correlation coefficients, the pairwise comparison matrix was the result of the joint consultation from three experts who are well acquainted with the preservation of earthen sites in China. After the joint consultation by the experts, they provided the final comparison results for the structured pairwise comparison matrices, as shown in Table 5. By calculating the CR, which represents the degree of consistency, such pairwise comparison matrices can be determined as consistent (CR ≤ 1.0).

Table 5 Pairwise comparison matrix, factor weights, the largest eigenvalues and CRs of the different layers

After acquiring all the initial data, the decision matrix C was determined as follows:

$$C = \left[ {\begin{array}{*{20}l} { 3 5. 9 6} & { 1 6. 4 7} & { 1 7. 9 8} & { 1 8. 7 2} & { 6. 5 5} & { 4 4. 9 6} & { 8 5. 0} & { 2 1 4 9. 0} & { 2 6. 7 7} & { 1 5. 4 0} & { 5 4. 1 9} & { 8 5. 0} & { 2 1 4 9. 0} \\ { 3 6. 7} & { 1 5. 7 3} & { 3 1. 9 5} & { 1 8. 4 7} & { 1 0. 5 7} & { 6 4. 4 8} & { 8 8. 4} & { 2 1 4 1. 4} & { 3 9. 9 3} & { 1 5. 0 9} & { 7 1. 1 7} & { 8 8. 4} & { 2 1 4 1. 4} \\ { 3 7. 5 9} & { 1 5. 0 1} & { 3 2. 9 6} & { 1 6. 4 3} & { 6. 4 4} & { 4 0. 9 7} & { 1 1 2. 3} & { 1 9 2 3. 4} & { 4 0. 8 9} & { 1 3. 1 1} & { 4 8. 1 1} & { 1 1 2. 3} & { 1 9 2 3. 4} \\ { 3 7. 7 4} & { 1 3. 4 7} & { 3 5. 0 9} & { 1 6. 7 9} & { 1 2. 2 6} & { 5 8. 4 9} & { 1 1 3. 6} & { 1 8 3 0. 4} & { 4 2. 1 1} & { 1 2. 5 6} & { 6 4. 5 8} & { 1 1 3. 6} & { 1 8 3 0. 4} \\ { 3 7. 5 5} & { 1 4. 8 6} & { 3 7. 0 2} & { 1 5. 7 6} & { 8. 1 1} & { 6 4. 3 5} & { 1 3 3. 0} & { 2 0 4 8. 0} & { 4 6. 2 7} & { 1 2. 7 1} & { 6 9. 8 2} & { 1 3 3. 0} & { 2 0 4 8. 0} \\ { 4 0. 5 6} & { 1 3. 0 7} & { 3 7. 7 7} & { 1 4. 1 6} & { 5. 2 1} & { 7 1. 8 6} & { 1 7 1. 0} & { 2 2 0 5. 0} & { 4 7. 9 1} & { 1 2. 4 1} & { 7 4. 9 5} & { 1 7 1. 0} & { 2 2 0 5. 0} \\ { 3 9. 0 1} & { 1 3. 5 8} & { 3 7. 9 2} & { 1 5. 1} & { 5. 7 0} & { 7 1. 0 1} & { 1 8 4. 0} & { 1 8 3 8. 0} & { 4 4. 1 5} & { 1 3. 0 5} & { 7 4. 1 7} & { 1 8 4. 0} & { 1 8 3 8. 0} \\ { 3 9. 8 5} & { 1 3. 1 1} & { 3 8. 7 2} & { 1 5. 3} & { 6. 9 7} & { 4 9. 9 7} & { 2 1 1. 6} & { 2 0 0 0. 6} & { 4 2. 4 8} & { 1 2. 0 4} & { 5 6. 4 6} & { 2 1 1. 6} & { 2 0 0 0. 6} \\ { 3 8. 9 1} & { 1 3. 2 7} & { 3 8. 1 7} & { 1 4. 5 7} & { 5. 3 7} & { 6 4. 8 5} & { 2 5 6. 0} & { 1 9 8 0. 0} & { 3 9. 6 8} & { 1 2. 2 8} & { 6 6. 8 1} & { 2 5 6. 0} & { 1 9 8 0. 0} \\ { 4 0. 8 6} & { 1 3. 3 7} & { 3 8. 2 2} & { 1 4. 3} & { 5. 2 0} & { 6 1. 9 3} & { 3 3 5. 4} & { 2 0 2 2. 3} & { 4 4. 7 4} & { 1 2. 0 4} & { 6 5. 3 3} & { 3 3 5. 4} & { 2 0 2 2. 3} \\ { 4 2. 0 8} & { 1 3. 0 6} & { 3 9. 7 1} & { 1 3. 7 9} & { 8. 3 1} & { 6 8. 6 8} & { 3 4 5. 0} & { 1 9 7 5. 0} & { 4 1. 9 6} & { 1 3. 0 8} & { 7 2. 3 2} & { 3 4 5. 0} & { 1 9 7 5. 0} \\ { 4 0. 9 8} & { 1 2. 9 4} & { 3 8. 6 1} & { 1 4. 6 4} & { 4. 4 9} & { 7 9. 9 1} & { 3 3 8. 5} & { 1 8 3 6. 3} & { 4 3. 5 6} & { 1 2. 1 6} & { 8 5. 7 3} & { 3 3 8. 5} & { 1 8 3 6. 3} \\ { 4 0. 9 1} & { 1 2. 7 1} & { 4 3. 5 1} & { 1 4. 0 8} & { 4. 9 8} & { 8 1. 9 3} & { 2 8 4. 0} & { 1 5 0 0. 0} & { 4 5. 6 9} & { 1 2. 4 4} & { 8 9. 2 2} & { 2 8 4. 0} & { 1 5 0 0. 0} \\ { 4 1. 5 4} & { 1 2. 8 7} & { 3 9. 3 7} & { 1 4. 3 5} & { 5. 8 2} & { 7 8. 3 0} & { 3 0 9. 0} & { 1 5 3 9. 0} & { 4 4. 3 2} & { 1 1. 7 0} & { 8 1. 9 6} & { 3 0 9. 0} & { 1 5 3 9. 0} \\ { 4 0. 1 2} & { 1 3. 5 4} & { 3 6. 3 3} & { 1 4. 3 9} & { 5. 0 9} & { 7 3. 7 9} & { 3 7 2. 0} & { 1 5 1 0. 0} & { 4 9. 4 0} & { 1 1. 5 9} & { 7 8. 2 8} & { 3 7 2. 0} & { 1 5 1 0. 0} \\ { 4 2. 6 5} & { 1 1. 7 1} & { 4 5. 3 2} & { 1 3. 5 1} & { 4. 5 1} & { 7 9. 2 4} & { 5 2 3. 3} & { 1 7 6 2. 8} & { 5 0. 3 7} & { 1 2. 4 2} & { 8 5. 5 4} & { 5 2 3. 3} & { 1 7 6 2. 8} \\ { 4 3. 3 5} & { 1 1. 7 4} & { 4 8. 6 8} & { 1 3. 5 2} & { 3. 7 7} & { 7 8. 8 2} & { 5 4 0. 9} & { 1 3 6 3. 6} & { 5 2. 4 3} & { 1 1. 4 9} & { 8 6. 2 8} & { 5 4 0. 9} & { 1 3 6 3. 6} \\ { 4 4. 3 6} & { 1 1. 9 4} & { 4 7. 7 1} & { 1 3. 3} & { 5. 1 5} & { 7 5. 9 2} & { 5 0 2. 5} & { 1 1 9 8. 3} & { 5 1. 9 2} & { 1 1. 6 3} & { 7 9. 5 2} & { 5 0 2. 5} & { 1 1 9 8. 3} \\ \end{array} } \right]$$

(17)

Then, it was normalized to form the normalized decision matrix E:

$$E = \left[ {\begin{array}{llllllllllllll} 1 &\quad 1 &\quad 1 &\quad 1 &\quad {0.327} &\quad {0.903} &\quad 1 &\quad {0.944} &\quad 0 &\quad 0 &\quad {0.148} &\quad 0 &\quad {0.056} \\ {0.912} &\quad {0.845} &\quad {0.545} &\quad {0.954} &\quad {0.801} &\quad {0.426} &\quad {0.993} &\quad {0.937} &\quad {0.513} &\quad {0.079} &\quad {0.561} &\quad {0.007} &\quad {0.063} \\ {0.806} &\quad { 0. 6 9 3} &\quad { 0. 5 1 2} &\quad { 0. 5 7 7} &\quad { 0. 3 1 4} &\quad 1 &\quad { 0. 9 4 0} &\quad { 0. 7 2 0} &\quad { 0. 5 5 0} &\quad { 0. 5 8 6} &\quad 0 &\quad { 0. 0 6 0} &\quad { 0. 2 8 0} \\ { 0. 7 8 8} &\quad { 0. 3 7 0} &\quad { 0. 4 4 2} &\quad { 0. 6 4 4} &\quad 1 &\quad { 0. 5 7 2} &\quad { 0. 9 3 7} &\quad { 0. 6 2 8} &\quad { 0. 5 9 8} &\quad { 0. 7 2 6} &\quad { 0. 4 0 1} &\quad { 0. 0 6 3} &\quad { 0. 3 7 2} \\ { 0. 8 1 1} &\quad { 0. 6 6 2} &\quad { 0. 3 8 0} &\quad { 0. 4 5 4} &\quad { 0. 5 1 1} &\quad { 0. 4 2 9} &\quad { 0. 8 9 5} &\quad { 0. 8 4 4} &\quad { 0. 7 6 0} &\quad { 0. 6 8 8} &\quad { 0. 5 2 8} &\quad { 0. 1 0 5} &\quad { 0. 1 5 6} \\ { 0. 4 5 2} &\quad { 0. 2 8 6} &\quad { 0. 3 5 5} &\quad { 0. 1 5 9} &\quad { 0. 1 6 9} &\quad { 0. 2 4 6} &\quad { 0. 8 1 1} &\quad 1 &\quad { 0. 8 2 4} &\quad { 0. 7 6 5} &\quad { 0. 6 5 3} &\quad { 0. 1 8 9} &\quad 0 \\ { 0. 6 3 7} &\quad { 0. 3 9 3} &\quad { 0. 3 5 0} &\quad { 0. 3 3 2} &\quad { 0. 2 2 7} &\quad { 0. 2 6 7} &\quad { 0. 7 8 3} &\quad { 0. 6 3 5} &\quad { 0. 6 7 7} &\quad { 0. 6 0 1} &\quad { 0. 6 3 4} &\quad { 0. 2 1 7} &\quad { 0. 3 6 5} \\ { 0. 5 3 7} &\quad { 0. 2 9 4} &\quad { 0. 3 2 4} &\quad { 0. 3 6 9} &\quad { 0. 3 7 7} &\quad { 0. 7 8 0} &\quad { 0. 7 2 2} &\quad { 0. 7 9 7} &\quad { 0. 6 1 2} &\quad { 0. 8 5 9} &\quad { 0. 2 0 3} &\quad { 0. 2 7 8} &\quad { 0. 2 0 3} \\ { 0. 6 4 9} &\quad { 0. 3 2 8} &\quad { 0. 3 4 2} &\quad { 0. 2 3 4} &\quad { 0. 1 8 8} &\quad { 0. 4 1 7} &\quad { 0. 6 2 5} &\quad { 0. 7 7 6} &\quad { 0. 5 0 3} &\quad { 0. 7 9 8} &\quad { 0. 4 5 5} &\quad { 0. 3 7 5} &\quad { 0. 2 2 4} \\ { 0. 4 1 7} &\quad { 0. 3 4 9} &\quad { 0. 3 4 1} &\quad { 0. 1 8 5} &\quad { 0. 1 6 8} &\quad { 0. 4 8 8} &\quad { 0. 4 5 1} &\quad { 0. 8 1 9} &\quad { 0. 7 0 0} &\quad { 0. 8 5 9} &\quad { 0. 4 1 9} &\quad { 0. 5 4 9} &\quad { 0. 1 8 1} \\ { 0. 2 7 1} &\quad { 0. 2 8 4} &\quad { 0. 2 9 2} &\quad { 0. 0 9 0} &\quad { 0. 5 3 5} &\quad { 0. 3 2 4} &\quad { 0. 4 3 0} &\quad { 0. 7 7 2} &\quad { 0. 5 9 2} &\quad { 0. 5 9 3} &\quad { 0. 5 8 9} &\quad { 0. 5 7 0} &\quad { 0. 2 2 8} \\ { 0. 4 0 2} &\quad { 0. 2 5 8} &\quad { 0. 3 2 8} &\quad { 0. 2 4 7} &\quad { 0. 0 8 5} &\quad { 0. 0 4 9} &\quad { 0. 4 4 4} &\quad { 0. 6 3 4} &\quad { 0. 6 5 4} &\quad { 0. 8 2 9} &\quad { 0. 9 1 5} &\quad { 0. 5 5 6} &\quad { 0. 3 6 6} \\ { 0. 4 1 1} &\quad { 0. 2 1 0} &\quad { 0. 1 6 8} &\quad { 0. 1 4 4} &\quad { 0. 1 4 2} &\quad 0 &\quad { 0. 5 6 4} &\quad { 0. 3 0 0} &\quad { 0. 7 3 7} &\quad { 0. 7 5 7} &\quad 1 &\quad { 0. 4 3 6} &\quad { 0. 7 0 0} \\ { 0. 3 3 6} &\quad { 0. 2 4 4} &\quad { 0. 3 0 3} &\quad { 0. 1 9 4} &\quad { 0. 2 4 2} &\quad { 0. 0 8 9} &\quad { 0. 5 0 9} &\quad { 0. 3 3 8} &\quad { 0. 6 8 4} &\quad { 0. 9 4 6} &\quad { 0. 8 2 4} &\quad { 0. 4 9 1} &\quad { 0. 6 6 2} \\ { 0. 5 0 5} &\quad { 0. 3 8 4} &\quad { 0. 4 0 2} &\quad { 0. 2 0 1} &\quad { 0. 1 5 5} &\quad { 0. 1 9 9} &\quad { 0. 3 7 0} &\quad { 0. 3 1 0} &\quad { 0. 8 8 2} &\quad { 0. 9 7 4} &\quad { 0. 7 3 4} &\quad { 0. 6 3 0} &\quad { 0. 6 9 0} \\ { 0. 2 0 4} &\quad 0 &\quad { 0. 1 0 9} &\quad { 0. 0 3 9} &\quad { 0. 0 8 7} &\quad { 0. 0 6 6} &\quad { 0. 0 3 9} &\quad { 0. 5 6 1} &\quad { 0. 9 1 9} &\quad { 0. 7 6 2} &\quad { 0. 9 1 1} &\quad { 0. 9 6 1} &\quad { 0. 4 3 9} \\ { 0. 1 2 0} &\quad { 0. 0 0 6} &\quad 0 &\quad { 0. 0 4 1} &\quad 0 &\quad { 0. 0 7 6} &\quad 0 &\quad { 0. 1 6 4} &\quad 1 &\quad 1 &\quad { 0. 9 2 9} &\quad 1 &\quad {0.836} \\ 0&\quad { 0. 0 4 8} &\quad { 0. 0 3 2} &\quad 0 &\quad { 0. 1 6 3} &\quad { 0. 1 4 7} &\quad { 0. 0 8 4} &\quad 0 &\quad { 0. 9 8 0} &\quad { 0. 9 6 4} &\quad { 0. 7 6 4} &\quad { 0. 9 1 6} &\quad 1 \\ \end{array} } \right]$$

(18)

Here, the authors started to evaluate the development of scaling off at the first site, JYG.

First, the relative membership R was calculated using fuzzy set theory according to Eqs. (11) and (12), which is shown:

$$R_{1} = \left[ {\begin{array}{*{20}l} 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ \end{array} } \right]$$

(19)

$$R_{2}=\left[ {\begin{array}{*{20}l} 1 &\quad 0 &\quad 0 &\quad 0 \\ 1 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad {0.809} &\quad {0.191} \\ 1 &\quad 0 &\quad 0 &\quad 0 \\ 1 &\quad 0 &\quad 0 &\quad 0 \\ 1 &\quad 0 &\quad 0 &\quad 0 \\ \end{array} } \right]$$

(20)

$$R_{3} = \left[ {\begin{array}{*{20}l} 0&\quad 0&\quad 0&\quad 1\\ 0&\quad 0&\quad{ 0. 0 9 1} &\quad { 0. 9 0 9} \\ 0&\quad 0&\quad 0&\quad 1\\ 0&\quad0&\quad 0&\quad 1\\ \end{array} } \right]$$

(21)

From Table 6, W_1i and W_2i can be acquired as follows:

$$W_{11} = \left[ {\begin{array}{*{20}c} { 0. 6 6 6 7} & { 0. 3 3 3 3} \\ \end{array} } \right]$$

(22)

$$W_{12} = \left[ {\begin{array}{*{20}c} { 0. 1 5 9 6} & { 0. 3 8 2 5} & { 0. 0 4 2 8} & { 0. 0 6 4 1} & { 0. 2 5 0 4} & { 0. 1 0 0 6} \\ \end{array} } \right]$$

(23)

$$W_{13} = \left[ {\begin{array}{*{20}c} { 0. 0 5 3 1} & { 0. 2 2 4 2} & { 0. 0 8 5 8} & { 0. 4 9 7 8} & { 0. 1 3 9 2} \\ \end{array} } \right]$$

(24)

$$W_{2i} = \left[ {\begin{array}{*{20}c} {0.6301} & {0.2184} & {0.1515} \\ \end{array} } \right]$$

(25)

Table 6 Comprehensive weights acquired by the AHP

Then, the comprehensive evaluation vector B_i can be established from Eq. (13).

$$B_{1} = W_{11} \times R_{1} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ \end{array} } \right]$$

(26)

$$B_{2} = W_{12} \times R_{2} = \left[ {\begin{array}{*{20}c} {0.9572} & 0 & {0.0346} & {0.0082} \\ \end{array} } \right]$$

(27)

$$B_{3} = W_{13} \times R_{3} = \left[ {\begin{array}{*{20}c} 0& 0 & { 0. 0 0 7 8} & { 0. 9 9 2 3} \\ \end{array} } \right]$$

(28)

Therefore,

$$B = \left[ {\begin{array}{*{20}c} 1&\quad 0&\quad 0&\quad 0\\ { 0. 9 57 2} &\quad 0&\quad { 0. 0 3 4 6} &\quad { 0. 0 0 8 2} \\ 0&\quad 0&\quad{ 0. 0 0 7 8} &\quad { 0. 9 9 2 3} \\ \end{array} } \right]$$

(29)

Then, the comprehensive evaluation T was obtained from Eq. (15).

$$T = W_{2i} \times B = \left[ {\begin{array}{*{20}c} {0.8392} & 0 & {0.0087} & {0.1521} \\ \end{array} } \right]$$

(30)

Finally, the comprehensive evaluation score of development H was calculated by Eq. (16):

$$H = T \times S^{T} = 0.7566$$

(31)

Thus, the degree of scaling off development in JYG is categorized as very high (VH).

Using the same procedures and methods, the scores and the degree of scaling off development at all 18 earthen sites can be calculated, as shown in Table 7.

Table 7 The degree of scaling off development at 18 earthen sites calculated via Fuzzy-AHP

Discussion

The characteristic values of scaling off were fit to the data on the engineering properties of rammed earth and the meteorological data from the occurrence environments. The porosity, shrinkage limit, clay contents and coarse silt contents of rammed earth were found to closely impact the development of scaling off, which are internal causes. Rainfall and evaporation also greatly influenced the development of scaling off, which are exterior causes.

In fact, the main rainfall pattern in this study area is the centralized type. After a precipitation event, the soil will quickly shrink under the heavy evaporative climates. From Fig. 9, the shrinkage limit of rammed earth in crusted layers is significantly larger than that in loose layers and host soil layers, causing nonuniform shrinkage between these layers. This condition will further accelerate soil cracking, which provides the prerequisite for the development of scaling off.

Fig. 9

The shrinkage limit of rammed earth in each layer

The development of scaling off is closely related to the weather conditions in NW China with the characteristics of brief but heavy rainfall, strong evaporation and a large difference in temperature between day and night. Precipitation can provide a carrier and momentum for soluble salt contained in rammed earth. The porosity plays a key role in determining the amount and degree of soluble salt migration. During rainfall, the soluble salt contained in the rammed earth will move from the crusted layers into the loose layers and host soil layers. As the salt content decreases, the clay content can increase, leading to a change in the particle size distribution of rammed earth, further influencing its engineering properties. Therefore, rainfall and porosity codetermine the longitudinal development of scaling off.

To explore the effects of particle size distribution, the authors measured the soluble salts in the crusted, loose and host soil layers (Fig. 10). Soluble salt was very unevenly distributed in these layers, and the crusted layers contained the least amount of soluble salts, which promoted the movement of the salts from the loose and host soil layers to the crusted layer. This condition is why there were many white crystalline substances aggregated in the interface between crusted and loose layers (Fig. 11). The approximate range of white crystals was outlined with a white curve. As the soluble salt in loose layers was apparently less than that in crusted layers, the salt migration mainly occurred between these two layers, so the thickness of crusted layers and loose layers represented the horizontal migration range. In this study, the particle size distribution was measured by adding a dispersing agent, sodium hexametaphosphate, with 4 wt% to eliminate the agglomeration effects of salt. To compare the salt agglomeration effects, the authors reconducted the test to measure the particle size distribution of rammed earth in crusted layers without adding the dispersing agent. Figure 12 indicates that the coarse silt contents greatly increased when dispersing agent was not added, and the clay contents simultaneously decreased under the same conditions. The addition of the dispersing agent eliminated the agglomeration effects of soluble salt. Therefore, this comparison proves that soluble salt influences the grain size distribution of rammed earth. Combined with the results of this test and the agglomeration effects of soluble salt, the authors inferred that the increase in coarse silt contents was due to the agglomeration effects of soluble salt, which causes more silt but less clay. Therefore, after the migration of soluble salt, these agglomeration effects would cause an increase in coarse silt, further reducing cohesive force, which provides a suitable condition for the development of scaling off.

Fig. 10

The soluble salt contents in each layer

Fig. 11

White crystalline substances aggregated at the interface between crusted and loose layers

Fig. 12

The comparison of particle concentration with/without adding the dispersing agent

The aridity can be calculated according to the ratio of evaporation to rainfall. As shown in Fig. 13, with the increase in drought, the development of scaling off becomes more serious. The degrees of scaling off development at earthen sites in extremely arid regions were very high or nearly very high, which are much more significant than the degrees of scaling off development in arid and semiarid regions. Conversely, the degrees of scaling off development at earthen sites in semiarid regions were low or nearly low. Most degrees of scaling off at earthen sites in arid regions were moderate, which falls between the scores for the extremely arid and semiarid regions. Therefore, the development of scaling off has a close relationship with aridity, which can be explained by the dual influence of rainfall and evaporation. In drought-prone regions, the amount of evaporation is extensive, causing the soils in crusted layers to shrink more quickly to accelerate the further development of scaling off.

Fig. 13

The relationship between scaling off development and aridity

Moreover, a sensitivity analysis was conducted to classify the porosity and shrinkage limit with strong subjectivity, as the classification of the porosity and shrinkage limit with strong subjectivity are relatively deficient compared with all other factors. The sensitivity analysis method that was applied mainly referred to the sensitivity analysis conducted in the risk assessment of seismic hazards in hydraulic fracture areas [22]. In this research, we used the mean value in Eq. (6) for the classification of membership (see C_M in Table 8). We replace the fourth, ninth, and fourteenth data values (in order from smallest to largest normalized data) as the classification boundaries and the 95% envelope interval of these three data values to carry out the sensitivity analysis (see C_1–3 in Table 8). The results of the sensitivity analysis of the porosity are shown in Fig. 14a. Black vertical lines indicate all the earthen sites with different assessment results after the corresponding sensitivity analysis. In addition, we used Mann–Whitney and Kolmogorov–Smirnov methods to evaluate these results (the p value should be greater than 0.05). From Fig. 14a, all the p values are greater than 0.05, meaning that the differences are not significant and our assessment is stable. In the same way, we conducted a sensitivity analysis and significance test for the shrinkage limits (Table 9). As shown in Fig. 14b, the p values were greater than 0.05, meaning that this parameter is also stable for evaluation.

Table 8 The classification of porosity value

Fig. 14

Sensitivity analysis of a porosity; b shrinkage limits

Table 9 The classification of shrinkage limits

Conclusions

We surveyed scaling off at 18 earthen sites in the field to determine and collect the characteristic values, namely, advantage area, the thickness of the crusted layer and the thickness of the loose layer. After that, the rammed earth in the crusted, loose and host soil layers was sampled to perform geotechnical tests to obtain engineering property data. Meanwhile, meteorological data were acquired. By fitting the characteristic values of scaling off with the data on the engineering properties of rammed earth and meteorological data, the influencing factors were determined. Then, the hierarchical structure of scaling off development was established, and Fuzzy-AHP was applied to evaluate the degrees of scaling off development at 18 earthen sites. From the results, we can conclude the following:

• 1. Scaling off exhibits a characteristic binary structure consisting of a crusted layer and a loose layer.

• 2. From the field investigation results of the plane and profile characteristics of scaling off, three characteristic values of scaling off, namely, advantage area, the thickness of the crusted layer and the thickness of the loose layer, were defined to characterize its degree of development.

• 3. The factors that influence scaling off were determined, namely, porosity, shrinkage limit, clay contents, coarse silt contents of rammed earth, rainfall and evaporation in the occurrence environments.

• 4. A hierarchical structure of the development of scaling off was established: the development of scaling off was defined as the goal layer; three characteristic values characterizing the development of scaling off made up the criterion layer; the index layer includes porosity, shrinkage limit, clay contents, coarse silt contents of rammed earth, and rainfall and evaporation in the occurrence environments.

• 5. The degree of scaling off development was calculated using Fuzzy-AHP, which indicated that as the level of drought increases, the development of scaling off becomes more serious. The degree of scaling off development in earthen sites in extremely arid regions was the highest, while that in semiarid regions was the lowest. The development scores of scaling off in arid regions fall between the scores in extremely arid and semiarid regions.

• 6. The agglomeration effects of soluble salt greatly influence the particle size distribution, which causes an increase in coarse silt, further reducing the cohesive force, which provides a suitable condition for scaling off development.