LBCapsNet: a lightweight balanced capsule framework for image classification of porcelain fragments

Abstract

The image classification task of porcelain fragments is of great significance for the digital preservation of cultural heritage. However, common issues are encountered in the image processing of porcelain fragments, including the low computation speed, decreased accuracy due to the uneven distribution of sample categories, and model instability. This study proposes a novel Capsule Network model, referred to as LBCapsNet, which is suitable for the extraction of features from images of porcelain artifacts fragments. A bottleneck-like channel transformation module denoted by ChannelTrans, which resides between the convolutional layer and the PrimaryCaps layer, was first designed. This module is used to reduce the computational complexity and enhance the processing speed when dealing with intricate porcelain images. The MF-R loss function was then proposed by incorporating focal loss into the original loss function. This allows to address the issue of imbalanced distribution of ceramic shard samples and reduce the classification errors, which leads to faster convergence with smoother trend. Finally, an adaptive dynamic routing mechanism is designed with a dynamic learning rate to enhance the overall stability of the classification process. The experimental results obtained on public datasets, such as MNIST, Fashion- MNIST, CIFAR10, FMD and DTD as well as porcelain fragments dataset, demonstrate that LBCapsNet achieves high classification accuracy with faster and more stable computation compared with existing methods. Furthermore, the ability of LBCapsNet to process special textures can provide technical support for the digital preservation and restoration of cultural heritage.

Introduction

Due to the passage of time and changes in burial conditions, porcelain artifacts [1] often fracture due to variations in soil pressure, resulting in a fragmented state when unearthed. The traditional methods for the classification of porcelain fragments [2] heavily rely on visual observations and experiential judgments, which are time-consuming and often require significant manual intervention. Some traditional machine learning classification methods [3], such as the decision tree [4], k-nearest neighbor [5], and support vector machine [6], often suffer from low generalization performance, susceptibility to noise interference, and low ability to process complex image data. With the continuous development of the image processing technology [7], the deep learning methods became able to improve the efficiency and accuracy while reducing the risk of secondary damage to cultural relics. Neural network models can be trained using a large dataset of known classified porcelain images for learning many features such as the morphology, patterns, and glaze colors of the porcelains. An accurate classification of porcelain artifact fragments can serve subsequent tasks such as the restoration [8] and repair of porcelains. It plays a crucial role in promoting cultural heritage preservation [9], digitization [10], and sustainable development. The existing deep learning classification methods for cultural relic fragments mainly include convolutional neural network (CNN) models [11], low-dimensional descriptors, unsupervised learning methods [12], pattern recognition algorithms [13], bimodal neural network models [14], and multiscale neural network models [15].

Compared with other image classification datasets [16], those composed of fragments of cultural objects have their own characteristics. In fact, the number of excavated porcelain fragments from cultural relics is often limited, and there may be considerable variation in the quantity of fragments across different categories, which leads to imbalanced samples within the dataset. In addition, the shape and size of the fragments vary, which hardens the functioning of common image processing methods. Moreover, the patterns of these fragments are complex and numerous. The patterns involved in the samples should be analyzed as a whole while considering their spatial relationship [17]. In this case, compared with CNN and other basic neural networks, the capsule network can better display complex features [18] such as the shape and texture of porcelain fragments.

Sabour et al. [19] introduced the concept of Capsule Networks (CapsNet) based on the idea of “capsules” proposed by Hinton et al. [20]. Within this conceptual framework, the fundamental element is referred to as a “Capsule”, which is a vectorized representation intricately capturing the spatial orientation and intrinsic characteristics of an object. In contrast to the neurons found in CNNs [21], these capsules possess a weight parameter that can be optimized through training. Furthermore, the capsules do not output scalar values; instead, they yield vector outputs, which allows to provide a more comprehensive representation of the underlying object. Compared with traditional CNNs, the capsule network offers several advantages. It succeeds in considering spatial relationships among objects from a vector perspective, and therefore it can effectively capture local features and global structures of objects. These characteristics make the capsule network particularly proficient in tasks such as debris classification and handwritten digit recognition. Moreover, the incorporation of capsule networks significantly enhances the accuracy and robustness of the model.

Significantly, the characteristic of viewpoint invariance inherent to capsule networks, as well as their approach to part-whole relationship processing, both play a positive role in the handling of objects, especially in the treatment of cultural relics such as porcelain artifact fragments.

In traditional neural networks, when input data undergoes rotation or translation, the network often needs to relearn the corresponding feature representations, leading to an inability to maintain stable recognition of the same object from different viewpoints. In contrast, within a capsule network, each capsule outputs a vector representing the current feature, which encapsulates not only the information about the feature itself but also its spatial relationship to other features, including position and orientation. Consequently, regardless of how an object is rotated or translated, the capsule network can adjust the inter-capsule relationships to maintain stable recognition of the same object. For instance, viewpoint invariance ensures that even if fragments of artifacts are presented at different angles, the system can still accurately identify and reconstruct the overall image of the relic.

Furthermore, there exists a dynamic routing mechanism between capsules in the network, allowing communication and interaction among different capsules, thereby capturing the connections between various parts of an object. Through this mechanism, capsules can learn local features of an object and combine these features to form a cognition of the whole object. This design enables the capsule network to better understand the structure and composition of an object, thus achieving accurate identification and reconstruction of the whole. For example, when processing fragments of cultural relics, the capsule network can learn different parts of the artifact (such as edges and decorations) and reconstruct the complete form of the relic through the part-whole relationship, playing a significant role in the digital preservation of cultural heritage.

Several issues exist in the image processing methods of porcelain shard, such as the low computational speed, imbalanced sample category distribution leading to decreased accuracy, and unstable model performance. Therefore, based on the CapsNets, this paper proposes a novel capsule network model referred to as the lightweight balanced capsule network for image classification of porcelain fragments (LBCapsNet). It has been demonstrated that CapsNets outperforms the CNNs in many image processing tasks, especially in enhancing the geometric transformation invariance and accurately modeling local structures. This advantage extends to specific tasks such as the identification and classification of cultural heritage fragments. To enhance the effectiveness of LBCapsNet in image classification, three key improvements are introduced. Firstly, lightweight processing techniques [22] are adopted to enhance the feature extraction ability and computational speed of the network. Secondly, the focal loss function is incorporated to improve the ability of the model to classify challenging samples. Finally, an adaptive learning rate adjustment mechanism is used to safeguard against model overfitting and gradient vanishing issues. Due to the incorporation of these enhancements, LBCapsNet demonstrates improved performance in accurately classifying porcelain fragments, and thus it contributes to the field of cultural heritage preservation and analysis. The incorporated improvements can be summarized as follows:

• 1. ChannelTrans: To enhance the feature extraction and computational speed of LBCapsNet, lightweight processing techniques are introduced to the convolution operation. By optimizing the convolutional layers, the parameter count and computational load are reduced while maintaining discriminative features. This improvement results in faster training and inference while retaining the high classification accuracy.

• 2. MF-R Loss function: The local loss function is incorporated into LBCapsNet to address the challenge of classifying complex samples, such as fragmented or deteriorated porcelain fragments images. This function assigns higher weights to misclassified difficult samples, which allows to emphasize their importance during training. This helps the model focus on learning challenging patterns and improves its ability to correctly classify such samples.

• 3. Adaptive learning Rate: To enhance the convergence speed and classification stability of the model, a dynamic learning rate calculation method, which specifically targets the coupling coefficients of dynamic routing, is introduced. The coupling coefficients are updated based on an adaptive learning rate, which gradually decreases with the increase of the iteration count. This approach allows to dynamically adjust the routing weights between capsules, and thus the overfitting issue can be prevented and the problem of vanishing gradients can be mitigated.

Related work

As previously mentioned, the classification of cultural relic fragments, including ceramics, is constantly evolving and improved in the deep learning field. Furthermore, in recent years, the capsule network framework developed by Sabour et al. [19] has been rapidly developed and has shown great potential in the image classification field.

Progress of the classification of cultural relics

With the continuous development of the image processing technology, deep learning-based techniques are increasingly applied to the classification of cultural relic fragments, including ceramic shards, terracotta warrior fragments, and cultural point clouds [23].

Chetouani et al. [24] employed a CNN model for automatic classification of ceramic shards. They also proposed a method for the classification of ceramic shard patterns by combining deep learning-based features extracted from some pre-trained CNN models. Similarly, Wu et al. [1] focused on the texture features of fragments and used a CNN for the classification and processing of ceramic tile textures. Ritz et al. [25] developed a pattern recognition-based algorithm that automatically extracts the relief features of each new object record, which allows to automate the classification process. Debroutelle et al. [13] also used automated pattern recognition to facilitate the interpretation of archaeological ceramic heritage. Gao et al. [12] proposed a three-dimensional cultural relic classification method based on low-dimensional descriptors and unsupervised learning for addressing the lack of sample labels or imbalanced sample distribution. Yang et al. [14] proposed a classification framework for three-dimensional terracotta warrior fragment data based on a bimodal neural network. This framework determines the categories of all the fragments by combining their geographical space and texture information. Liu et al. [15] proposed an attention-based multi-scale neural network for fragment classification, which is referred to as AMS-Net, while focusing on the geometric and semantic features of the fragments.

The existing classification methods employed for cultural relic fragments [26] encounter practical challenges such as data scarcity and imbalanced samples, as well as technical issues such as low ability to extract deep-level features and difficulty in fully utilizing spatial structure and local feature information. Addressing these challenges is imperative to promptly enhance and optimize the current methods.

Development of CapsNet

Capsule networks have rapidly evolved [27] in the machine learning field due to their innovative solutions addressing challenges such as object rotation and scaling. However, they also have some drawbacks. For instance, due to the fact that the dynamic routing mechanism requires multiple iterative computations, and each capsule necessitates the learning of a transformation matrix for predicting the state of the next-layer capsule, the capsule networks have high computational load, large number of parameters, and potentially unstable training. Consequently, Hinton et al. [28] designed the Expectation–Maximization (EM) routing algorithm. In addition, there incorporated attention mechanisms into the process. Zhang et al. [29] proposed a relation extraction method based on attention-based capsule networks for enhancing the extraction of relationships among multiple entities. Mazzia et al. [30] modified the capsule network by incorporating a self-attention routing mechanism, which results in a streamlined structure with only 160000 parameters.

Besides image processing, the approach of capsule networks is also adopted in various other domains. For instance, Kim et al. [31] applied the principles and techniques of capsule networks to text classification, while employing static routing and using ELU gates for information propagation. Their results showcased the reliability and efficacy of capsule networks in the text classification field. In the 3D model processing field, Zhao et al. [32] proposed a 3D point cloud capsule network.

Application of CapsNet in classification

Withing the various task categories, exploring capsule networks proves valuable for classification tasks due to their ability to hierarchically model features. This enables the encapsulation of attitudes, relationships, and spatial structures of objects.

In recent years, several improved capsule networks have been proposed and applied to image classification tasks. For instance, Nair et al. [33] designed an incremental stress-testing method that provides a more in-depth recording of its internal embedding space and sources of error, in order to better understand the performance and representational capacity of CapsNet. Xiang et al. [34] proposed a multi-scale capsule network referred to as MS-CapsNet, consisting of two stages for enhancing the expressive power of the capsule network. Rajasegaran et al. [35] proposed a deep capsule network referred to as DeepCaps, which introduces a novel dynamic routing algorithm based on three-dimensional convolutions to assist in learning. In addition, DeepCaps incorporates a novel class-agnostic decoder network with controllable instantiation parameters, which effectively enhances the performance of the capsule network when dealing with complex image datasets. Yang et al. [36] proposed RS-CapsNet to tackle the challenge posed by complex background images. This approach leverages Res2Net blocks [37] for extracting multi-scale features and employs Squeeze-and-Excitation (SE) blocks for emphasizing useful features while suppressing irrelevant ones. Huang et al. [38] proposed DA-CapsNet, which improves the hierarchical structure of the capsules by incorporating attention mechanisms to form an activation capsule with dual attention. He et al. [39] designed a novel capsule network referred to as MRCapsNet, which improves the hardware-friendliness and allows the deployment on edge devices. This network adopts a multi-level residual capsule block structure for the extraction of multi-granularity features from images. In addition to these aforementioned examples, more CapsNets are still emerging.

Nevertheless, the capsule network image classification methods face problems that cannot be ignored [40]. They should simultaneously learn the pose and feature information of instances, which often leads to increased training difficulty and computational complexity. In addition, when dealing with small sample data, the training of capsule networks lacks sufficient parameters and data, which easily causes overfitting or underfitting.

LBCapsNet method

The LBCapsNet model presents significant advancements for the classification of porcelain fragments. The integration of lightweight processing techniques, focal loss function, and adaptive dynamic routing mechanism contribute to the increase of the feature extraction ability, classification accuracy, and practicality in real-world image classification tasks. This section provides a comprehensive overview of LBCapsNet, followed by a detailed description of the lightweight block, loss function, and dynamic routing.

Overview

The overall architecture of LBCapsNet is shown in Fig. 1. In image classification problems, the mathematical objective of this study is to map an input image to a discrete class label. Thus, a mathematical model that extracts effective features from the input data and uses them for the classification task, is designed to minimize the classification error rate of the model.

Fig. 1

An overview of the LBCapsNet

The proposed network structure includes convolutional layers, channel transformation layers, primary capsule layers, digit capsule layers with dynamic learning rate routing algorithms, and reconstruction layers. These components function together to transform the input data into a high-dimensional feature representation, calculate weights through dynamic routing algorithms, generate prediction vectors, and map capsule representations back to the original image through the reconstruction layer. In addition, a loss function that incorporates focal loss is defined to measure the difference between the model output and the true label.

At the outset of the network, PrimaryCaps act as the foundational capsule layer, tasked with extracting feature information from input data and transmitting it to subsequent layers. Each PrimaryCap encompasses multiple capsule units, each dedicated to a distinct feature or pattern found in the input data. By learning the organization of these features or patterns, PrimaryCaps capture the structured information embedded within the input data. Conversely, DigitCaps represent the advanced capsule layer within the Capsule Network, serving to encode feature vectors corresponding to different categories. Each DigitCap aligns with a specific category and learns to discern the features characteristic of that category. Leveraging a dynamic routing algorithm, DigitCaps ascertain the relevant capsules from the preceding layer (PrimaryCaps), establishing inter-category relationships and producing feature vectors that encapsulate each category.

The “Reconstruction layer” in the network structure is a decoder composed of fully connected (Linear) layers, designed to reconstruct the original input image from the feature vectors outputted by the Digital Capsule layer (DigitCaps layer). This process aids in understanding the main content and features within the image. As shown in Fig. 1, ReLU functions are used between the three fully connected layers to introduce non-linearity and assist the model in learning complex image reconstruction mappings; the final layer employs a Sigmoid activation function since the pixel values of the images to be reconstructed typically range between 0 and 1.

The training process begins with input data (i.e., images) being fed into the model. Firstly, the basic features of the images are extracted using an initial convolutional layer, followed by a non-linear transformation using the ReLU activation function. These features are then refined further through a channel transformation module, which includes structures such as convolutions and residual blocks. This helps enhance the expressive power of the model while controlling the number of parameters. The processed features are passed through the PrimaryCaps layer, where multiple convolutional units generate a series of capsules. Each capsule is a vector representing the existence and parameters of specific features in the image. These capsules are then fed into the DigitCaps layer using a dynamic routing mechanism, which adjusts the connection weights between input and output capsules based on their similarity. This determines the contribution of each input capsule to the output capsules. Each output capsule represents a category, with the length of its vector indicating the probability of that category’s presence.

After obtaining the output from the DigitCaps layer, the model performs two tasks: first, it calculates the length of each output capsule to determine the image’s category; second, it uses selected capsule vectors to reconstruct the original image through a decoder. After each forward pass, the model evaluates its performance by computing a loss function. This loss function combines a margin loss for classification accuracy and a reconstruction loss for image quality. The gradients of the loss with respect to the model parameters are then computed using backpropagation, and an optimizer is used to update the weights and biases of the model to minimize the loss.

This training process is repeated on the training set for multiple epochs until the model achieves satisfactory performance or meets other stopping conditions. Throughout the training process, the model continuously learns and adjusts its parameters to better accomplish the tasks of image classification and reconstruction, ultimately achieving the goal of recognizing and understanding the content of the images.

In summary, the proposed network architecture leverages advanced techniques, such as capsule networks and dynamic routing algorithms, to effectively extract features from input data for image classification tasks. The obtained results demonstrate improved accuracy compared with traditional CNNs, highlighting the potential of the proposed network for further development in this field.

Lightweight block

Figure 1 shows the structure of the proposed model, where the lightweight channel between the capsule network's original convolution layer and PrimaryCaps is embedded. This channel is referred to as ChannelTrans. It represents a convolutional neural network layer designed to learn the underlying features of input data. Figure 2 illustrates a more detailed structure of ChannelTrans.

Fig. 2

An overview of the ChannelTrans

A 1 × 1 convolutional layer is first employed to reduce the number of channels [41] in the input feature map to 128. A normalization procedure and the ReLU6 activation function are then applied to the processed data. Afterwards, a 3 × 3 convolutional layer is used for downsampling, while incorporating group convolution on the channel dimension, which enhances the nonlinearity and receptive field of the model. The normalization procedure and the ReLU6 activation function are employed again to ensure high data stability and gradient robustness. To mitigate the network degradation and improve the feature representation ability, the ResidualBlock module, which consists of two consecutive 3 × 3 convolutional layers and a 1 × 1 convolutional layer, is incorporated. This arrangement allows to learn more expressive features and alleviates the problem of vanishing gradients. Finally, a 1 × 1 convolutional layer is used to expand the channel dimension back to 256. To ensure the high consistency of the data, the normalization procedure and the ReLU6 activation function are applied again. In general, this module demonstrates high feature learning ability and stability in data handling.

In contrast to the commonly used bottleneck structure, adjustments are made to the ChannelTrans architecture. In the aforementioned module, replacing the Batch Normalization (BN) with Instance Normalization (IN) [42] for processing porcelain data leads to several improvements, as shown in Fig. 3. Porcelain data are typically represented as individual samples, where each sample represents an independent piece. In this scenario, IN is better suited for handling individual samples as it performs normalization across the channel dimension. This allows for better feature extraction and representation, as it captures the unique characteristics of each fragment. In addition, the size and shape of porcelain fragments can be different. BN often requires a large batch size to perform stable normalization [43]. However, in cases where the number of fragments is limited, attaining a large batch size becomes challenging. Adopting IN can alleviate this issue, as it performs normalization on the channel dimension of each sample, regardless of the batch size. This makes it more adaptable to different sizes and shapes of porcelain fragments. Furthermore, by normalizing within the channel dimension of individual samples, IN maintains the differences between samples, which allows to more easily and accurately capture the unique decorative characteristics of each fragment. A previous study states that compared with BN, IN is more suitable for tasks that require preserving individual sample features. Thus, using IN can better capture the differences and characteristics among the porcelain artifact fragment data. Consequently, replacing BN with IN when processing porcelain fragment data can lead to several improvements, including better adaptation to individual samples, varying sizes and shapes, as well as more accurate feature extraction. These aspects contribute to the enhancement of the performance and effectiveness of the model. However, the specific effects should be evaluated based on the characteristics of the dataset and the underlying task.

Fig. 3

Structural comparison. a Common Bottleneck. b Our ChannelTrans

The ResidualBlock module is designed to alleviate the vanishing gradient problem and improve the training effectiveness of the model by incorporating residual connections [44, 45]. It consists of two convolutional layers and two BN layers. The two convolutional layers employ 3 × 3 filters with a stride of 1 and a padding of 1 in order to perform convolutions on the input feature maps, while the BN layers are used to normalize the convolutional outputs. During the forward propagation, the input feature map is first stored in a variable denoted by “residual”, which is then added to the output of the convolutional operations. Afterwards, the input feature map is processed through the first convolutional layer, BN layer, and ReLU activation function. The resulting feature map is then processed by the second convolutional layer and batch normalization layer. Furthermore, the output of the convolutional layer is combined with the original input feature map to form a residual connection. This allows to preserve the initial information and mitigate the information loss and gradient vanishing. Finally, a ReLU activation function is applied to introduce non-linearity before outputting the processed feature map.

In this study, ReLU6 is a variation of the Rectified Linear Unit (ReLU) function [46], which sets all negative values to zero, but also sets all positive values greater than 6–6. This introduces a capped linear behavior for input values above 6. The function is often used in deep learning models, especially in situations where a bounded activation range is desired. This constraint allows to maintain a robust nonlinear capacity, which contributes to the stabilization of the neural network training.

Loss functions

In the classification of porcelain fragments of cultural relics, sample imbalance often exists in the underlying datasets. That is, the number of samples in some categories is significantly larger than that in other categories. This kind of unbalanced samples [47] leads to the poor learning effect of the classifier for the few categories in the training process, and it can be easily misclassified into the most categories.

To solve this problem, focal loss [48], which is an improved loss function, can be introduced into the classification framework. It is a loss function for unbalanced samples, which makes the network pay more attention to the hard-to-classify samples by reducing the weight of the easy-to-classify ones.

It can adjust the weight of each sample by introducing a moderator. The moderating factor is related to the category of the samples. More precisely, focal loss introduces a tuning factor known as the focusing parameter, typically denoted by γ. This focusing parameter allows for the adjustment of weights for each sample, leading to varying contributions to the loss for different samples. For easily classifiable samples, their predicted probabilities are higher, and the focusing parameter reduces the weight of these samples, thereby reducing their impact during training and preventing the model from overly emphasizing these samples. Conversely, for difficult-to-classify samples with lower predicted probabilities, the focusing parameter increases their weight, causing the model to pay more attention to these challenging samples and thereby enhancing the model's learning ability for them. Therefore, during the training process, the focal loss can pay more attention to few categories of samples, and improve the classification accuracy of hard-to-classify samples. Compared with the traditional cross-entropy loss function, it can effectively solve the problem of sample imbalance in the debris classification field. In addition, it can improve the classification performance of the model for a small number of categories, and increase the attention to the hard-to-classify samples.

The conventional forms of the margin loss and focal loss calculations are respectively shown in Eqs. 1 and 2, which serve as a reference in this study.

$$\begin{gathered} L_{{{\text{margin}}}} = \sum {\left[ {T_{c} \max \left( {0,m^{ + } - {\text{logits}}} \right)^{2} } \right.} \hfill \\ \, \left. { + \alpha \left( {1 - T_{c} } \right)\max \left( {0,{\text{logits}} - m^{ - } } \right)^{2} } \right] \hfill \\ \end{gathered}$$

(1)

where T_c represents the score for the target category c, also known as logits, which is essentially the model’s predictive output for each category. The term m⁺ is the margin threshold for positive groups. If the score is lower than m⁺, it will result in a loss, forcing the model to push up the score of the correct group. Similarly, m⁻ is the margin threshold for negative groups. The parameter α is an adjustable weight, which can balance the impact of losses between positive and negative groups.

$$L_{{{\text{focal}}}} = - \alpha \cdot \left( {1 - p_{t} } \right)^{\gamma } \cdot \log \left( {p_{t} } \right)$$

(2)

where p_t represents the model’s predicted probability for the current group, which serves to adjust the focal loss. If a sample belongs to the positive group, then p_t = p; otherwise, p_t = 1—p, where p is the output probability for the positive group. The α acts as a balancing factor, aimed at helping to focus more on the minority group in scenarios of sample imbalance. In addition, γ regulates the model’s emphasis on samples that are easy or difficult to classify. As γ increases, the loss attributed to well-classified samples (i.e., those with p_t close to 1) is significantly reduced, thereby encouraging the model to pay more attention to samples that are hard to classify correctly.

In the proposed method, the margin loss (L_mar) is computed as:

$$L_{{{\text{mar}}}} = \sum\limits_{i = 1}^{n} {\left[ {y_{i} \cdot {\text{left}}_{i} { + }\,\alpha \cdot \left( {1 - {\text{y}}_{i} } \right) \cdot {\text{right}}_{i} } \right]}$$

(3)

where left represents the margin loss for the correctly classified samples, right represents the margin loss for the misclassified samples, i denotes the sample count, y_i represents the true label of the sample, and α is a hyperparameter used to adjust the weight of the false positive loss.

Prior to the calculation of the focal loss (L_foc), an exponential decay factor (p_t) for L_mar is first calculated as:

$$p_{t} = {\text{e}}^{{ - L_{mar} }}$$

(4)

L_mar is then combined with p_t to obtain the deformed L_foc:

$$L_{foc} = \alpha \cdot \left( {1 - p_{t} } \right)^{\gamma } \cdot L_{mar}$$

(5)

where α is a hyperparameter used to adjust the weight of the false positive loss, and γ is the exponential factor controlling the decay rate of the focal loss.

Afterwards, the reconstruction loss (L_rec) (Fig. 4) is calculated using the mean square error (MSE) between the reconstructed input data and the original input data:

$$L_{rec} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {r_{i} - \hat{r}_{i} } \right)^{2} }$$

(6)

where $r_{i}$ denotes the input, and $\hat{r}_{i}$ represents the output from the reconstruction network.

Fig. 4

Our loss function

Afterwards, L_foc and L_rec are combined to obtain the overall loss function (L_MF-R):

$$L_{MF - R} = L_{foc} + \lambda \cdot L_{rec}$$

(7)

where λ is a balance coefficient that can balance the effects of L_foc and L_rec.

Finally, the total loss is the result of dividing the L_MF-R by the batch size.

Compared with the original loss function of the capsule network, the new one enhances the performance of the model in addressing class imbalance and trade-off. The key differences and advantages are summarized as follows:

The introduction of focal loss in the loss function effectively addresses the issue of class imbalance. By adjusting the weights assigned to negative samples, the focal loss focuses on difficult-to-classify samples, which allows to improve the learning ability of the model for specific categories. In contrast to the original boundary loss of the capsule network, the focal loss combines the exponential form and the boundary loss of the predicted outcome. Consequently, it separately calculates the focal loss for each sample and category, and aggregates them accordingly.

In addition, the new loss function incorporates parameter adjustments. The α parameter is used to fine-tune the weight relationship between positive and negative samples in the focal loss, while the λ parameter modulates the degree of focus within the loss function. By appropriately adjusting these parameters, the performance of the model can be further enhanced, ensuring that increased attention is given to difficult-to-classify samples.

Furthermore, the new loss function takes into account the weight of the reconstruction loss. This adjustment achieves a balance in the contribution of the boundary loss and the reconstruction loss, which allows the model to simultaneously learn boundary information while retaining high reconstruction ability.

In summary, the MF-R loss function significantly enhances the capacity to address performance class imbalance and trade-offs. By incorporating the focal loss, adjusting the underlying parameters, and optimizing the weighting of the reconstruction loss, the model places greater emphasis on challenging samples. This approach intensifies learning for specific categories, balances the contributions of margin loss and reconstruction loss, and increases the overall performance.

Routing algorithm

In the proposed original dynamic routing mechanism, a dynamic learning rate [49] approach was introduced to adaptively adjust the coupling coefficients. Parameter lr represents a dynamically adjusted learning rate, which controls the convergence speed and stability of the model. It changes at each iteration step, while decreasing based on the number of iterations. Using a larger initial learning rate, the model can undergo faster initial learning and then gradually decrease the learning rate to enhance the stability. This dynamic adjustment of the learning rate helps to prevent overfitting and gradient vanishing issues. Parameter α is used for regularization, which allows to remove the existing noise and improve the stability of the model. At each iteration step, the coupling coefficient b_ij is updated by subtracting α multiplied by itself. This process allows to suppress the excessive growth of coupling coefficients between capsules, and therefore model overfitting can be prevented. The regularization strength can be controlled by adjusting the value of α, which allows to balance the fitting ability and generalization performance of the model.

The concept of “adaptiveness” is also introduced. More precisely, in each dynamic routing iteration, the output vector is calculated and the coupling coefficients are updated based on their current values and the input samples. This iterative process allows to adaptively adjust the parameters of the model and better fit the features of the input data.

Algorithm 1

The proposed adaptive dynamic routing algorithm

The entire process of dynamic routing is shown in Algorithm 1. The input vectors undergo a series of steps including linear transformation, coupling coefficient updates, weighted summation, and non-linear activation functions to yield the output of capsules. More precisely, at each iteration step, the input vectors undergo linear transformation by performing matrix multiplication with the weight matrix W of the capsules, in order to determine the tensor u representing the capsule output. The output vector b_ij of the capsule is then initialized to zero, and the coupling coefficients c_ij are computed based on the output vector b_ij, representing the correlation or weight between the input vector x and the capsule. Afterwards, the output vector u of the capsules is weighted summed using c_ij to obtain the summarized output vector s_j. A non-linear activation function, such as the squash function, is applied to s_j in order to obtain the final output vector of the capsule v_j. At each iteration step, the change in the coupling coefficient Δb_ij is computed based on v_j and the input vector u, while the dynamic learning rate lr and regularization parameter α are used to update b_ij. Finally, the ultimate output result of the capsule v is obtained by compressing the output vectors.

The dynamic learning rate adjustment mechanism is important in the machine learning field as it allows to adaptively adjust the learning rate based on data characteristics and model training dynamics. Within the context of dynamic routing, this mechanism is crucial for effectively adapting to the complexity and diversity of the input data. The dynamic routing process consists in dynamically selecting paths or adjusting information transmission modes within a neural network based on the characteristics of the input data. By dynamically adjusting the learning rate, the mechanism allows to better control over the strength and direction of information propagation, which facilitates the improved adaptation to the change of the input data.

Results and analysis

This section shows and analyzes the performance of LBCapsNet in terms of classification accuracy, trends in the loss function, and average computation speed per epoch.

Datasets

To evaluate the overall performance of LBCapsNet, image classification experiments are conducted on the MNIST, Fashion-MNIST, CIFAR10, FMD, and DTD datasets, and the accuracy of the obtained results is compared with those of other classical network frameworks. The MNIST and Fashion-MNIST datasets are composed of 70,000 grayscale images having a size of 28 × 28 × 1 and divided into 10 different classes. 60,000 and 10,000 images are used for training and testing, respectively. The CIFAR10 dataset comprises 60,000 images having a size of 32 × 32 × 3 (the last dimension denotes the 3 color channels) and divided into 10 different classes. 50,000 of these images are used for training, while the remaining 10,000 are used for testing. The Flickr Material Dataset (FMD) comprises 1,000 images with a size of 512 × 384 representing 10 different material classes, 800 of these images are used for training, while the remaining 200 are used for testing. The Describable Textures Dataset (DTD) consists of 5640 texture images distributed across 47 different classes, 4512 of these images are used for training, while the remaining 1128 are used for testing.

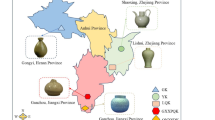
In addition, tests were performed on the porcelain shard dataset built in this study in order to demonstrate its high effectiveness. This dataset consists of 1045 fragments of celadon/blue and white porcelain, categorized into six groups based on the shades of color—Q1 to Q6, representing light, medium, and dark tones, as shown in Fig. 5. The fragments were captured from multiple angles using a high-resolution Sony digital camera. In order to enrich the dataset, various techniques, including translation and rotation, were adopted to reach approximately 8,000 images. After adding appropriate labels, this dataset represents a two-dimensional collection of porcelain fragment images. It is then divided into training and testing sets following a ratio of 3:2.

Fig. 5

Datasets used in this work. a MNIST. b Fashion-MNIST. c CIFAR10. d FMD. e DTD. f Our dataset

Setup

PyTorch is used to develop and implement the LBCapsNet, and the experiments are performed in CPU and RTX-4080 environments. The experiments involving the CPU were conducted using an 11th Gen Intel Core i7-1165G7 processor, which operated at a base frequency of 2.80 GHz. During the training process, the initial learning rate is set to 0.0001, and the model undergoes training for 64 epochs.

The experiments utilized an improved version of the CapsNet model, namely LBCapsNet, and were based on MNIST, Fashion-MNIST, CIFAR10, FMD, DTD and laboratory porcelain shard datasets for training and testing. The introduction of this model aims to enhance the performance of traditional convolutional neural networks in image processing by learning the spatial hierarchical relationships within images. This model, through capsule-based methods, retains more spatial information, demonstrating superior performance in image recognition tasks.

During training, the Adam optimizer was employed. Furthermore, an exponential decay learning rate scheduler with a decay factor of 0.96 was adopted in the experiments, aimed at gradually reducing the learning rate as training progressed, leveraging its adaptive learning rate to help the model converge more stably in later stages of training. Regarding the loss function, the L_MF-R loss function was selected to mitigate the issue of sample imbalance, considering both reconstruction error and classification error to enhance the overall performance of the model. Additionally, random cropping and normalization of images were applied during training to increase the model's generalization ability. The batch size was set to 128, with training spanning over 64 epochs. In each iteration, model performance was monitored by calculating average loss and accuracy, using accuracy and average training time per epoch as the primary evaluation metrics.

Ability of image classification

In terms of image classification accuracy, the conducted comparison mainly focuses on two categories of network models: classical CNN models such as AlexNet, VGG, DenseNet, and ResNet, and improved capsule network models such as MS-CapsNet, RS-CapsNet, and DeepCaps.

It can be seen from Table 1 that LBCapsNet has stable performance when dealing with public datasets, which highlights the superiority of the fundamental framework of the capsule network in image processing tasks. In addition, although its image classification accuracy on MNIST (99.68%) is slightly lower than that on CapsNet’s (99.75%), LBCapsNet still achieves high accuracies on Fashion-MNIST (94.58%) and CIFAR10 (91.32%), which are higher than those of most of the recent improved capsule networks.

Table 1 Classification test accuracy across 3 publicly available image datasets after 64 epochs

It can be observed from Table 2 that LBCapsNet also achieves high performance when dealing with the material, texture and porcelain shards dataset. Moreover, it can be deduced from the results of the last three ablation experiments that the ChannelTrans module has a greater impact on LBCapsNet compared with the L_MF-R loss module. Furthermore, the improvement of the classification accuracy of our dataset due to the L_MF-R loss module indirectly demonstrates its effectiveness in addressing the imbalance in the number of samples for different categories of porcelain shards. Compared to the FMD and DTD datasets, our dataset exhibits this aspect more prominently, as the former two are inherently balanced.

Table 2 Classification test accuracy on FMD, DTD and our image dataset of porcelain fragments in our laboratory after 64 epochs

Performance of the loss function

Figure 6 shows the loss curves of baseline-CapsNet and LBCapsNet on MNIST, Fashion-MNIST, and CIFAR10 over 64 epochs.

Fig. 6

Loss comparation on three datasets. a MNIST. b Fashion-MNIST. a CIFAR10

Compared with baseline-CapsNet, LBCapsNet has higher initial loss due to its more complex network structure. However, LBCapsNet has a higher convergence speed. The trend of the loss curve also indicates a smoother convergence for LBCapsNet, highlighting its stability when applied to public datasets. These imply that LBCapsNet is capable of achieving optimal performance more rapidly as training progresses and shows better reliability in convergence, making it a good choice for image classification tasks.

Comparison between the computational loads

Time-based tests were conducted on the MNIST, Fashion-MNIST, CIFAR10, FMD, and DTD datasets using the same parameter settings, in the regular CPU environment and the corresponding CUDA environment for RTX-4080. The average time consumptions per epoch under the respective conditions are shown in Table 3. The magnitude of this indicator allows for a direct comparison between the computational loads of LBCapsNet and CapsNet. This comparison is visually intuitive and highlights the advancements in speed achieved by LBCapsNet.

Table 3 Assuming all other conditions are held constant, the average computation time per epoch (in seconds) was measured for 5 publicly available image datasets as well as our own dataset, in both CPU and GPU environments

It can be seen that CapsNet has lower image classification speed in the CPU environment, while the proposed LBCapsNet consumes less than half the time on average per epoch, which greatly improves the experimental efficiency. In the GPU environment, LBCapsNet also has lower computational load. On the MNIST, Fashion-MNIST, CIFAR10, FMD, DTD and our porcelain datasets, the average computation time per epoch are only 5.73, 6.19, 9.49, 5.91, 66.27 and 49.08 s, respectively. Although LBCapsNet takes more time compared to AlexNet and ResNet in many cases, it has been able to minimize the time difference and achieve comparable speeds while preserving the core functionality of capsule networks. In comparison to VGG, LBCapsNet demonstrates faster computational speed. When facing practical demands in the processing of cultural heritage data, a higher computational speed facilitates the procedures involved in the field of cultural heritage preservation.

Conclusion

With the continuous development of the digital preservation technology for cultural heritage, the digital classification of cultural relic fragments has become increasingly significant. This paper proposes a capsule network model designed for the classification of porcelain cultural relic fragments, which is referred to as LBCapsNet. A lightweight channel transformation module, denoted by ChannelTrans, is first designed. It incorporates residual blocks between the convolutional layer and the PrimaryCaps layer. This module improves the computational speed and reduces the risk of overfitting due to the residual blocks. The MF-R loss function is then designed with focal loss characteristics to remove the classification errors caused by the imbalanced distribution of porcelain fragment samples. In addition, the concept of dynamic learning rate is incorporated into dynamic routing, which allows to update the coupling coefficients through adaptive learning rates. The experimental results demonstrate that compared with existing methods, LBCapsNet achieves higher classification accuracy, lower computational load, and more stable computation in handling image datasets including a porcelain fragment dataset.

However, some problems are encountered during the training process. For instance, in extreme cases, the model may learn unreasonable parameters or rules, which leads to Not-a-Number (NaN) conditions in the loss function. Consequently, an effective training becomes unattainable, which indicates a form of numerical instability and model fragility. Therefore, considering the needs of digital preservation for cultural heritage, a future study can be conducted on the following aspects: (1) Applying the methodology to porcelain fragments that are not blue or white in order to evaluate the scope of its applicability. (2) Investigating whether other lightweight network architectures are suitable for the classification of porcelain fragments. (3) Transferring the classification approach from two-dimensional fragment analysis to three-dimensional fragment categorization. (4) Finding and developing methods to further enhance the stability of the model. In fact, a deep learning-based method for the classification of porcelain fragments can identify their category and help performing subsequent tasks such as fragment stitching and age determination.