Abstract
Traditional methods for ancient mural segmentation have drawbacks, including fuzzy target boundaries and low efficiency. Targeting these problems, this study proposes a pyramid scene parsing MobileNetV2 network (PSP-M) by fusing a deep separable convolution-based lightweight neural network with a multiscale image segmentation model. In this model, deep separable convolution-fused MobileNetV2, as the backbone network, is embedded in the image segmentation model, PSPNet. The pyramid scene parsing structure, particularly owned by the two models, is used to process the background features of images, which aims to reduce feature loss and to improve the efficiency of image feature extraction. In the meantime, atrous convolution is utilized to expand the perceptive field, aiming to ensure the integrity of image semantic information without changing the number of parameters. Compared with traditional image segmentation models, PSP-M increases the average training accuracy by 2%, increases the peak signal-to-noise ratio by 1–2 dB and improves the structural similarity index by 0.1–0.2.
Similar content being viewed by others
Introduction
With the continuous development of computer software and hardware, as well as the gradual deepening of social informatization, cultural relic protection institutions have introduced advanced digital technology to iteratively update traditional technology, while improving the work efficiency of relevant workers, reducing workloads and enhancing the values of traditional culture. As a traditional cultural carrier, ancient murals play an important role in Chinese culture, and their contents reflect the charm of traditional Chinese culture from multiple aspects, such as the geographical environment and local traditions and customs. However, due to its long history, traditional Chinese murals, represented by Dunhuang murals and Liaoyang Han Tomb murals, have experienced serious damage artificially and by the natural environment. As a consequence, only a small number of murals have been completely preserved, and most murals are confronted with a series of problems, such as content defects and color loss, which pose a great threat to ancient mural protection.
The first step for mural image digital protection is to understand the image. Influenced by traditional culture, ancient Chinese murals are characterized by bright colors and rich content. Analyzing the image is one of the most difficult problems in Chinese mural image protection. Image segmentation is an important method for image understanding. This technique can divide an image into several noninteractive regions according to grayscale, color and texture. The consistency or similarity between image features can then be mapped out through these regions. As different regions have different exhibitions, this technique calibrates them based on the discontinuity of the gray levels at their boundaries to achieve image analysis. After image segmentation, the image elements in the murals are classified to determine the specific meaning of each image element. When all the elements of the murals are clear, a deep understanding of the connotation and historical value of the images can be achieved, thereby promoting the development of traditional culture in contemporary times. However, to date, no image segmentation models can be perfect enough to use universally, and therefore, proper model selection plays a crucial role in ancient mural image segmentation.
Currently, ancient image segmentation remains in the stage of the use of traditional methods, and techniques from the field of deep learning have seldom been involved. Most of the traditional methods can process gray images, but they are not applicable for ancient mural images, whose colors are abundant. Some of the commonly used traditional methods are as follows: The Fuzzy C-means (FCM) [1] is a clustering algorithm in the field of machine learning. Its principle is to enable the target function to maximize the similarities among the objects of the same cluster, while also reducing the connections among the different clusters. This algorithm has been widely applied, and a related mature theoretical system has been formed. However, when used for ancient mural image segmentation, the FCM does not take spatial information into consideration, and it is sensitive to noise and grayscale unevenness. In addition, it is influenced by sample imbalance, leading to differences between the segmented samples and the target samples. Although the fusion of wavelet frames [2, 3] and particle swarm optimizers [3] with the FCM is able to reduce calculation complexity and the principles behind them are simple and easy to carry out, these fusion methods are likely to cause the loss of the diversity of image elements, therefore resulting in local optimization of the segmented image. Otsu [4] is a modified threshold-based algorithm. The basic idea behind this algorithm is that image data is classified according to thresholds. Compared with the FCM, Otus has the virtue of a lower probability of pixel errors, but it struggles with higher calculation complexity and a larger amount of computation. K-means [5, 6] is another widely applied unsupervised learning algorithm. Its working principle is as follows: The K number of cluster centers is selected for classification according to the image pixel, and then the clustering centers are redemarcated until the positions of the centers do not change or the set number of iterations is reached. The drawbacks of this algorithm are obvious. First, the K value is artificially selected; the value is influenced by subjective factors. Second, after the evaluation function of the algorithm converges, the clustering is complete. During this process, continuous iteration is required, and the outcomes obtained can only represent locally optimized outcomes, whereas the effect of global segmentation is poor. Graph cuts [7] and its modified algorithm Grab Cut [8] are also two commonly used methods for mural image segmentation. Both algorithms adopt one-time minimization and iterative minimization to optimize the parameters of the gray histogram based on the target and background of the Gaussian mixed model (GMM) [9], thereby achieving a satisfactory segmentation effect. However, for ancient mural images whose composition is complex, the segmentation outcomes of both algorithms are poor. In addition, if the user specifies a pixel as the target, the segmentation outcomes of both algorithms will be affected. Machine learning methods can be divided into generation and discrimination methods, which correspond to generation models and discrimination models, respectively. Among generation models, the most popular is generative adversarial networks (GANs) [10]. GANs have been widely adopted for image segmentation because they do not need Markov chain repeated sampling or require inference in the learning process. These features successfully evade the difficult probability problem of pixel approximation calculation. However, GANs also have disadvantages that cannot be ignored. First, the GAN network is difficult to train because it has no loss function, and therefore, it is difficult to determine whether progress has been made during the training process. Furthermore, GAN may collapse in the learning process, and the generator may begin to degrade, always generating the same sample points and cannot continue learning. These disadvantages make the experiment unable to continue. The mean shift [11] algorithm is based on the mean shift, and it is essentially a kernel density estimation algorithm. The drawback of this algorithm is that its running speed is low. It is only applicable for the feature data point set with established standard features, and in the meantime, it is likely to have images other than the target or miss some targets.
In recent years, the rapid development of deep learning has changed the previous manner where machine learning describes image features. It utilizes a neural network system to combine the low-level features of an image to form abstract high-level features. Additionally, it uses these features to represent the attribute class of image elements and to discover the representation of the distribution feature of the data. Through layer-by-layer feature transformation, it transforms the feature representation of the sample in the original space to a new feature space, thereby simplifying image segmentation and classification prediction. In the field of image segmentation, the frequently used models include fully convolutional networks (FCNs) [12], segment networks (SegNet) modified based on the FCN [13] and a DeepLab series of networks proposed by Chen et al. [14, 15]. China is a country with a long history. However, research on ancient Chinese mural image segmentation is rare. Even among the small number of reported studies, most focus on the exploration of the traditional segmentation methods and fail to deeply explore the adaptability of semantic segmentation models based on deep learning in mural segmentation neighborhoods. In addition, most of the segmentation objects are single channel gray images, which has certain limitations on RGB images.
According to the complex composition of ancient mural images, as we leverage the powerful learning capacity of the deep learning network, we propose a new model that can be applied in image segmentation for ancient mural images, the pyramid scene parsing MobileNetV2 Network (PSP-M), by fusing a deep separable convolution network with the spatial pyramid pooling modules of the scene parsing model, PSPNet [16]. The advantage of the PSP-M lies in its fusion of a spatial pyramid structure with multiscale image information, which enables it to be applicable for feature extraction from ancient mural images. In this model, the deep separable convolution network used is MobileNetV2 [17,18,19]. As a typical lightweight neural network, MobileNetV2 is the most representative convolution network containing a deep separable structure. The utilization of MobileNetV2 for feature extraction improves the efficiency for mural image segmentation and reduces the influence of hardware constraints on segmentation. The pyramid pooling structure in the PSP-M network connects the generated different features smoothly onto a fully connected layer for information extraction from different regions of the image. In addition, we introduce the loss function, Dice loss function [20], for multipoint analysis of the image region, which reduces the impact of sample imbalance on the outcomes of mural image segmentation, and therefore, effectively overcomes the drawbacks of the FCM algorithm. The employment of convolutional neural networks for image feature extraction eliminates the influence of artificial factors in the K-means algorithm and graph cut algorithm on experimental outcomes. Furthermore, PSPNet has the virtue of global priority, which contains information at different scales from different subregions, and therefore, it outperforms the K-means and graph cut in terms of segmentation effect.
Methods
Background theories
Atrous convolution
Image feature extraction by the PSPNet involves the use of atrous convolution [21]. The convolution operation is a process of image feature extraction, and the number of convolution kernels determines the number of extracted features. The operation principle is that a mathematical operator generates the third function based on two functions. FCN, a frequently used image segmentation network, utilizes a pooling layer and a convolution layer to expand the perceptive field, and in the meantime, the size of the feature map is reduced, which is recovered using the upsampling method. However, the recovery process can cause a loss of accuracy. To solve this problem, the concept of atrous convolution is proposed. The new convolution method is a modification of the traditional convolution method, where the concept hole is introduced. The convolution treats the output feature map y as the dependent variable and the corresponding independent variable x as the input feature map. Parameters that influence y include the convolution kernel w and the dilation rate r. If a position on the feature map y is defined as i, the equation can be obtained as follows:
The atrous convolution performs sampling on the original graph, and the sampling frequency is closely related to the dilation rate. When the dilation rate is = 1, the information contained in the original graph can be completely preserved, without information loss, and under such a condition, the convolution operation is considered the standard convolution operation. A dilation rate > 1 indicates that sampling is performed with an interval of dialation rate-1 pixels on the original image. For example, for a 3 × 3 convolution, when the dilation rate is set at 1, 2 and 3, the obtained images can be seen in Fig. 1a–c.
As shown in Fig. 1, when the dilation rate is 1 for a 3 × 3 convolution, the convolution kernel can be considered a common convolution with a size of 3 × 3; when the dilation rate is 2, the convolution kernel turns to 5 × 5; and when the dilation rate is 3, the convolution kernel becomes equivalent to a 7 × 7 convolution kernel. The size of the equivalent convolution kernel of the atrous convolution Ki is related to the atrous convolution kernel K as follows:
where d represents the hole number. If the product of the strides of all previous convolutions (except for the current layer) is represented as Si, then the stride of the convolution layer refers to the number of rows and columns in each sliding process of the convolution kernel. The equation can be obtained as follows:
If RFi+1 represents the current perceptive field and RFi represents the perceptive field of the preceding layer, the equation can be obtained as follows:
Based on Eqs. (2), (3) and (4), with kernel = 3 and stride = 1, atrous convolutions are consecutively performed at dilation rats of 1, 2 and 4 [22], and the receptive fields of the first, second and third layers are 3 × 3, 7 × 7 and 15 × 15, respectively.
The special parameter of atrous convolution, the dilation rate, defines the distance between values when the convolution kernel processes data. It increases the receptive field of the convolution kernel while keeping the number of parameters unchanged, which ensures that the size of the output feature map remains unchanged.
Deep separable convolution
Deep separable convolution was first proposed in the MobileNetV1 framework [23], which involves two dimensions, i.e., space and depth, simultaneously. Its operation contains two parts, i.e., depthwise convolution (DW) and pointwise convolution (PW). The workflow of deep separable convolution is shown in Fig. 2.
Figure 2a shows the input channels of the standard convolution, Fig. 2b shows the DW convolution for different channels, and Fig. 2c shows the PW fusion of the convolution results. If the size of the input feature map is defined at DF × DF × M and that of the output map is DF × DF × N, the amount of calculation of standard convolution DK × DK can be calculated as follows:
In deep separable convolution, the amount of calculation of DW is as follows:
and the amount of calculation of PW is as follows:
Therefore, the total calculation amount of the deep separable convolution is as follows:
The ratio between the deep separable convolution and the standard convolution can be calculated as follows:
Under the conditions of the size of the convolution kernel of 3×3 with a large number of channels N, deep separable convolution decreases the calculation amount by 90% compared with standard convolution. Given the same number of parameters, the neural network with deep separable convolution possesses a deeper network structure, which can improve efficiency without noticeably decreasing accuracy.
To better show the workflow of the deep separable network, a three-channel image at 5 ×5 pixels is introduced, and the convolution process is shown in Fig. 3. As shown in Fig. 3, during convolution, each convolutional kernel is responsible for a channel, and each channel is convoluted by only one convolutional kernel. Convolution is operated on a two-dimensional plane. First, one-time convolution is operated, and the number of convolutional kernels is the same as the number of channels of the preceding layer. After the operation, the three-channel image forms three feature maps. In Fig. 3a, the process is illustrated. The input is an image in RGB format, which is transformed into a feature map through filter convolution. In the region designated by Fig. 3a, a filter only contains a kernel of size 3×3. After convolution, the obtained number of feature maps is the same as the channel number of the input layer, and therefore, feature maps are not expanded in number. Furthermore, this operation convolutes each channel of the input layer independently and does not effectively use the feature information of different channels in the same spatial position. Therefore, pointwise convolution is required to combine the feature maps to form new feature maps (Fig. 3b). The operation for pointwise convolution is very similar to that of conventional convolution, and the size of its convolutional kernel is 1 × 1 × M, where M represents the number of channels of the preceding layer. Therefore, the convolution operation at this step weighs and combines the previous feature maps in the depth direction to generate new feature maps. After pointwise convolution, similarly, four feature maps are output. Although the output dimension is the same as that of conventional convolution, the total calculation amount is one-third that of conventional convolution.
Operational principle of a deep separable network. a Depthwise convolution. b Pointwise convolution. The input is a three-channel color image. The image undergoes depthwise convolution (a) to obtain a feature map (maps*3) on the two-dimensional plane, which further undergoes pointwise convolution (b) to form a feature map (maps*4). This treatment aims to effectively take advantage of different channels to obtain the features at the same spatial position
MobileNetV2 network
The proposal of the MobileNetV2 convolutional neural network aims to solve problems, such as an excessively large convolutional neural network and insufficient hardware training during the image model training process. It is an important way for deep learning models to release the memory limitation of the hardware deployed at the mobile terminal. In addition, it is another important invention following lightweight neural convolution networks, such as squeeze networks (SqueezeNet) [24], shuffle networks (ShuffleNet) [25] and Xception [26]. The core part of MobileNetV2 is the deep separable network.
Based on the first-generation lightweight network mobile network vision 1 (MobileNetV1), the concepts of inverted residuals and linear bottlenecks are introduced into MobileNetV2 [27]. As a DW convolution cannot change the number of channels, feature extraction is restricted by the number of input channels. Inverted residuals and linear bottlenecks take low-dimensional compression as the input, expand it to high dimensions, and then filter it through lightweight depth convolution. The obtained features are projected through linear convolution into low dimensions for representation. The network structure of MobileNetV2 is summarized in Table 1.
In each sequence, there is a stride at the first layer, and the strides of the remaining layers are all 1. All spatial convolutions involve a convolution kernel with a size of 3 × 3. Each bottleneck contains three parts, i.e., expansion, convolution and compression. Each row describes one or multiple sequences with n repetitions. Within each sequence, all layers contain the same number of output channels. MobileNetv2 allows us to considerably reduce memory occupation in the reasoning process through incompletely materialized intermediate tensors. When applied to mural segmentation, it can reduce the demand for main memory access in most designs of embedded hardware.
PSP-M model
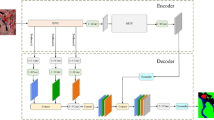
PSPNet uses a residual network (ResNet) as its grassroots network [28]. The original PSPNet model employs ResNet and atrous convolution to extract the feature map of an image and uses a pyramid scene parsing network to embed scene information that is difficult to parse by a computer in the prediction framework, thereby completing the calibration for appointed image regions and achieving a satisfactory semantic segmentation effect. With ResNet as the grassroots network, the PSPNet model exhibits satisfactory training performance. With the increase in network depth, however, the extra problems of optimization difficulty increase the complexity of the segmentation model and restrict the employment of the model at the mobile terminal. To solve this problem, we integrate the lightweight neural network with a deep separable structure MobileNetV2 in the PSPNet model. This design greatly reduces the number of parameters in the network and increases the adaptability of computer hardware. The modified model is shown in Fig. 4.
PSP-M mural segmentation model. The foundation layer of the input image is subjected to pretraining by MobilNetV2 and atrous convolution treatment to extract feature map (a), which is further processed by the pyramid pooling module, represented by b in the figure, to obtain the fused features with global information. The features are fused with feature map (a) and then output through convolution (3)
In the proposed model, the image feature extractor ResNet (residual convolution neural network; indicated by (1) in Fig. 4) is changed to a lightweight convolution neural network for the extraction of the feature map from the input image. All output images are three-dimensional tensor RGB images, whose resolutions are 224 × 224. A deep separable convolution network is used to extract the feature pixels of the mural. With one convolution kernel corresponding to the convolution of one channel, convolution calculation is performed for each channel in the input layer. The number of channels of the feature map is equivalent to that of the input layer. Afterward, the previously processed features experience weighted combinations through point convolution in the depth direction. The channels are transformed. The transformed feature map undergoes dilated convolution (dilation rate = 3) to obtain feature map (a). Till now, the backbone work is completed. A new feature map (indicated by (a) in Fig. 4) is generated, and the calculation amount of the neural network is reduced.
The proposed model changes the way that the convolution network in the traditional model is activated by the ReLU function in the low-dimensional space [29]. ReLU is capable of saving the complete information of the input manifold only when the input manifold is located in the low-dimensional subspace of the input space. According to Tang et al. [26], a linear layer can prevent damage to image information caused by nonlinear functions. Therefore, in the proposed PSP-M model, linear transformation is used to replace the original ReLU activation when the number of image channels is small, and thus, the loss of image features is reduced.
PSP-M changes the three-stage feature extraction manner in traditional segmentation methods, i.e., dimension reduction followed by a convolution and dimension increase. It fuses inverted residual modules and adopts the manner of dimensions increasing followed by a convolution and dimension reduction. The utilization of the shortcut structure enhances the gradient propagation capability between multilayer networks, matched with longitudinal convolution to transfer feature extraction to high dimensions. The advantage of this operation is that the scale of convolution kernels is much smaller than the number of output channels, which can reduce the time and spatial complexity of the convolution layer. This design is memory-friendly and greatly improves the segmentation efficiency of the model.
Finally, the model also exhibits optimization in detail, such as the choice between Maxpool and Avgpool [30]. Because the objects of ancient mural segmentation models prefer texture contour features, maximum pooling is selected as the pooling method of the model, which filters image irrelevant feature information, and thus, makes the mural segmentation effect more distinct. In addition, at the part labeled (2) in the figure, a deep separable convolution network is also introduced, which spans two to three network layers in a shortcut mode. With reference to the residual network model, the problem of increased feature extraction errors caused by gradient divergence in deep models is solved, thereby improving the accuracy of feature segmentation as a whole. The features after multiscale fusion through pyramid global modules are extracted and then further fused with (a). After the results are obtained, the number of channels is reduced, the model training complexity is reduced, and the final prediction map is generated through the convolution modules of structure (3).
The workflow of the model is shown in Fig. 5.
PSP-M workflow. The input image is subjected to deep separable convolution to form a feature map, which further undergoes maximum pooling and processing with the pyramid pooling module to obtain the semantic information of feature maps. Then, upsampling is performed for the image containing the semantic information using bilinear interpolation. Finally, feature maps of different hierarchies are spliced up to obtain the predicted image
The workflow of the algorithm is described as follows:
Step 1: We input the image.
Step 2: We take advantage of the longitudinal convolution and point convolution in MobileNetV2 to extract the feature information of the input image. Then, we form a feature map.
Step 3: We perform maximum pooling for the feature map and use four-layer pyramid modules to obtain context information. The sizes of the pooling kernels of the four layers correspond to the features of the whole feature image, 1/2 of the image and a small part of the image. These features can form the global features of the image after fusion.
Step 4: We perform direct upsampling on the low-dimension feature map through bilinear interpolation to recover the original size of the feature map at each layer of the global pyramid modules.
Step 5: We splice the feature maps at different levels into the final global feature of pyramid pooling.
Step 6: We generate the final prediction map after a convolution layer. The segmentation workflow ends.
The fusion of a lightweight neural network in the PSP-M model improves the efficiency of image segmentation and guarantees segmentation accuracy. It also greatly decreases the number of parameters required for model calculation, reduces the requirements for hardware conditions in the process of pretraining, and reduces the learning cost of the neural network. These virtues allow the proposed model to eliminate the dependence on large and medium-sized equipment, improve the matching degree with light equipment, and achieve a satisfactory effect on mural segmentation.
The pseudocodes of PSP-M are as follows:
Input: the training set, Dataset, the testing set, Image and the segmentation model, Model.
-
1.
Logs ← ModelTrain(Dataset); /*train Dataset by PSP-M, place the parameters into the Logs files*/
-
2.
PredictLoad(Logs); select the optimal parameters from Logs and introduce them into the prediction procedure*/
-
3.
Image_out Model(Image); Segment the images in Image*/
Output: Segmented image set Image_out.
Experiment
Experimental environment
The experiment is performed on the Window 10 operating system, with Inter Core i7-9750H as the PC processor, NVIDIA GeForce 1660Ti as the graphics card, JetBrains PyCharm Community Edition 2019 as the platform and with Python as the language. Based on the TensorFlow1.11.0 deep learning framework, combined with the Keras2.2.4 library, the proposed model is trained and tested. The computer vision and machine learning software library, Opencv, and the labeling software, Labelme, are used for dataset processing.
Experimental objective
The purpose of the current experiment is to test the feasibility of the application of the PSP-M model in image segmentation for ancient Chinese mural images, and the performance of the PSP-M is tested by comparing those of other models.
Experimental design
The datasets for the experiment are divided into the training set and the testing set. The datasets contain six types of labels, with a total of 500 images, which are all from Complete Works of Dunhuang Murals in China and the scanning graphs of Wutai Mountain mural images. These images, belonging to different types and with different sizes, are modified to images with a resolution of 224 × 224 with the resize function provided by OpenCV, and the obtained images are integrated into the original dataset. The dataset required for network model training in the field of deep learning should contain thousands of images. To solve the problem of overfitting due to a small dataset in the process of image segmentation, the dataset experiences enhancement (data augmentation). Specifically, Scikit-image is used to implement the data enhancement commands for rotation and flipping. Image layers are modified using Photoshop, the color-scale tool is employed to darken images with a complex composition structure, and the filter function of the software is used to add noise to the original image. The number of images in the dataset is expanded to 2000 (Additional file 1). The training and testing datasets are divided according to a ratio of 9:1. Detailed information on the enhanced dataset is summarized in Table 2. The six labels for these images include animal, house, people, auspicious clouds specifically associated with Buddhism and the Buddha statue, and apart from background.
The enhancement effect is shown in Fig. 6.
The PSP-M requires single-channel labeled images as the dataset. After data enhancement, the main foreground of each image is subjected to point-by-point annotation with image labeling software.
An example of the annotation effect is given in Fig. 7.
Figure 7a shows the scanned image. Its edges are subjected to point-by-point annotation with floating points. These annotation points are connected to form the result shown in Fig. 7b. Then, a single-channel gray image is trained according to the original and annotation images. The obtained gray images and the scanned images are merged to form the dataset.
In terms of the loss function, a cross entropy loss function and the Dice loss function are employed in the PSP-M. The cross-entropy loss function independently evaluates the class prediction of each speed limit vector and then averages the pixels. If sample imbalance appears, the weight of the smaller target sample is reset until a satisfactory segmentation effect is achieved. The loss change is shown in Fig. 8.
In the PSP-M, the Dice loss function is also used separately. The principle of the Dice coefficient is to intersect the predicted result with the real result. The obtained value is multiplied by two and divided by the sum of the absolute values of the predicted result and the real result. To reflect the convergence of the loss function, the Dice loss function is taken as 1 minus the value of the Dice coefficient. Such an operation can overcome the negative influence caused by the different sizes of the images. In the training process, we pay more attention to the foreground region of the image to eliminate the possible impact of sample imbalance on the segmentation results. The Dice loss function change is shown in Fig. 9.
In the training process, every 10 epochs compose one generation. The size of batch_size is set at 8, and batch is extracted 250 times per generation for 250 parameter updates. The learning rate is 1e-5. A callback function, ReduceLROnPlateau (parameters: foctor = 0.5, patience = 3, verbose = 1.it), is used to monitor the loss values of the training set and the testing set. If three continuous values do not decrease, the learning rate is reduced. If more than three of the continuous loss values do not decrease, the model training process ends. The variations in the segmentation accuracy of the model show a decrease followed by a rather stable state (Fig. 10).
As shown in Fig. 10, the accuracy of the segmentation model improves rapidly in the first three generations, fluctuates in the fifth and sixth generations, and stabilizes again after the eighth generation. The training of the model ends in the tenth generation, and the learning rate reaches an optimal level.
Results and discussion
Comparison of the amount of parameters
To validate the satisfactory performance of the lightweight neural network with a deep separable structure MobileNetV2 in image segmentation, comparisons are made with some of the frequently used traditional network models, and the results are summarized in Table 3.
In common neural network models, a higher depth value of the model means a greater number of parameters, a more complex structure, and a greater difficulty in training. As shown in Table 3, the parameter amounts of Xception [25], Visual-Geometry-Group 19 (VGG19) [31], ResNet50 [32] and IceptionV3 [33] are several-fold that of MobileNetV2, and even ResNet50, which is one of the typical ImageNet programs, and has more than 2 times the parameter amount compared with MobileNetV2. These findings, combined with a comprehensive analysis of other factors, such as experimental hardware requirements and training time, indicate that the selection of a convolutional neural network with a deep separable structure for ancient mural segmentation is reasonable.
Comparison of the time for segmentation
To validate the satisfactory performance of the deep separable network in segmenting the neighborhood regions of the ancient mural image, we assess the proposed model in terms of segmentation time, accuracy and segmentation effect. First, based on the self-prepared datasets, the traditional image segmentation models FCM [1] and Grapth Cuts [6], the currently typical image segmentation network models in the field of deep learning SegNet [13], PSPNet [16] and DeeplabV3 + [15] and the modified DeeplabV3 + -based model MC-DM [34] are selected. Then, the results of time consumption for segmentation are compared (Table 4).
To compare the results obtained in this study with those reported in the literature [1, 7], all models are operated in CPUs other than the GPU environment. As shown in Table 4, the traditional FCM model has the longest time consumption, whereas that of the Grapth cuts model is the shortest. However, Grapth Cuts has blurred segmentation boundaries and chaotic backgrounds and foregrounds. Compared with other models, its segmentation effect is much poorer. To achieve a satisfactory effect, a large number of target points must be annotated artificially, which requires a much longer time compared with other models. DeepLabV3 + is one of the best models in the field of image segmentation. It employs the encoder-decoder [35] structure, which is able to fuse the feature information of the image at multiple scales, and thus, reduce the loss of the spatial information of the image. However, due to a rather complex structure, it takes a long time to predict the results. MC-DM is a modified model based on DeeplabV3 + . It integrates a lightweight neural network in the original model, and therefore, reduces the limitations of hardware conditions and improves the work efficiency of the model. However, its segmentation efficiency is much lower than that of the PSP-M model. In addition, the PSPNet selects the residual neural network, ResNet50, as the basic network, and the PSP-M uses MobileNetV2 as the basic network layer. The PSP-M model outperforms the PSPNet in segmentation efficiency.
Comparison of the accuracy
In terms of pixel accuracy (PA) [36], FCM and K-means (clustering algorithm) have low sensitivity to color, and thus, they are often used for gray image segmentation. The accuracy of Grapth Cuts in image segmentation varies according to the quality of the images provided by the users, and it is influenced by artificial factors. Therefore, in this study, we compare the accuracy of the PSP-M with those of the SegNet [13], PSPNet [16], DeepLabV3 + [15] and MC-DM [34]. The results are summarized in Table 5.
The SegNet calculates the pooled index using the maximum pooling method, by calculating the nonlinear upsampling of the corresponding encoder, thereby saving the upsampling learning process. However, for mural segmentation, this model cannot make full use of the relationship between image pixels, and thus, it lacks context-based reasoning ability due to the complex composition of mural images. The PSPNet is characterized by global priority. It contains the global pyramid module with information about different subregions at different scales. The fusion of four types of pyramid-scaled features helps solve the image understanding problem when faced with complex scenes. It increases the accuracy by 1% compared with the SegNet network. The DeepLabV3 + adopts Xception as the underlying network, and its combination with the spatial pyramid module ASPP restores the spatial information of the image, which optimizes the segmented boundaries of the image. With the modified underlying network and different designed loss functions, the PSP-M solves the sample imbalance problem in the segmentation process, which optimizes the feature extraction module of the model and saves segmentation time. In terms of accuracy, the PSP-M is close to the MC-DM, but it is slightly lower than the DeepLabV3 + . Its accuracy is 2% higher than that of the PSPNet and 3% higher than that of the SegNet.
Comparison of the segmentation effect
To intuitively perceive the segmentation effects of different models, we randomly select mural images from four different categories for semantic segmentation. With the segmentation of a single category of mural images as the baseline and other image elements as the background, we perform pixel-level image annotations for the segmentation results. The comparative results are shown in Fig. 11.
In Fig. 11, the first row shows the scanned mural images, and the second row shows the outlined annotated images based on the anchor points annotated by image annotation software. The remaining rows show the image segmentation effects of different models. The SegNet is one of the early models adopting the encoder-decoder structure. Its continuous downsampling enables the model to compress image features into tiny image indices. However, this operation can lead to overlap among image spatial information. In addition, after continuous upsampling, the image presents problems, such as a lack of central information and discontinuous edges of the segmented images. The fusion of the residual neural network and the introduction of residual blocks improve the performance of the PSPNet but increase the network width indirectly, which decreases the computing power of the model. Although the edge continuity of the segmented images based on the PSPNet improves compared with the SegNet, central detail defects do appear when the PSPNet is used to segment the images from a single category. The segmentation effect of Grapth Cuts is optimized with the increase in the number of artificially annotated points. Its segmentation effect is greatly affected by artificial factors, and therefore, can only be used for reference. Because of the integration of the spatial pyramid module and the encoder-decoder structure, DeepLabV3 + achieves a satisfactory segmentation effect. However, with the increase in the depth of the network, the expansion of the parameter space and the increase in training difficulties, it is likely to be affected by overfitting. As a consequence, its segmentation effect becomes unstable. The fusion of the lightweight neural network reduces the number of parameters in the MC-DM model and reduces the time required for its training. For this reason, MC-DM achieves great improvement compared with other models. However, in regard to image details, much improvement remains to be made. While reducing the number of parameters, the PSP-M solves the image segmentation problem caused by sample imbalance.
In addition, we use subjective assessment [37], the peak signal-to-noise ratio (PSNR) [38] and the structural similarity (SSIM) [39] as the assessment indices to compare the segmentation results of the model proposed in this study with those of other models.
To investigate the subjective assessment of the performance of the proposed model, we assign 1, 2, 3 and 4 to four scanned images. We prepare images based on the segmentation results of different models. A total of 100 studies are randomly selected, and the best segmentation results are recorded. The statistical results are shown in Fig. 12.
As shown in Fig. 12, 38% of the subjects believe that PSP-M achieved the best segmentation effect, followed by the MC-DM (32%). Due to individual differences in the segmentation effect, the DeepLabV3 + is only supported by 8 students, although it achieves the best accuracy during training. The SegNet and the PSPNet receive the lowest support rates.
Currently, the PSNR is the most common and widely used index for image evaluation. A larger value indicates a higher similarity between images. We suppose two images satisfy \(x,y \in R^{n \times m}\), where x is the noise approximation of y, X(i,j) and Y(i,j) represent the pixel values of the corresponding coordinates, H and W represent the height and width of the image, and n is the bit of each pixel. The PSNR is defined as follows:
The RSNRs of the four samples based on different models are summarized in Table 6.
During the experiment, the SegNet and the PSPNet exhibit stable performance. For sample 2, which has a distinct outline and a simple structure, the segmentation effects of the six models are comparable. However, in samples 1 and 3, whose compositions are relatively complex, the DeepLabV3 + exhibits polarization in the segmentation effect. The MC-DM and the PSP-M show relatively satisfactory performance. The PSNR value of the PSP-M is 1–2 dB higher than that of MC-DM. The segmentation results of Grapth Cuts are affected by human factors, and its PSNR value can only be used as a reference.
Because the sensitivity of human vision to errors is not absolute and its perception results are affected by a variety of factors, such as the surrounding environment and light perception, there is a phenomenon of pleasant subjective feeling with a low PSNR value. Therefore, another assessment index is introduced in our study, i.e., SSIM. The calculation formula of SSIM is as follows:
where uX and uy represent the mean X and Y values of the image, respectively, σX and σY represent the standard deviations of the X and Y values of the image, σXσX and σYσY represent the variances of X and Y, respectively, σXY represents the covariance of X and Y, and C1, C2 and C3 are constants, which are meant to avoid a 0 denominator. Similarly, SSIM is an index that is used to assess the similarity between two digital images. Compared with the PSNR, the measurement of SSIM in the quality of the image structure is more consistent with the judgment based on human vision. The SSIM value ranges from − 1 to 1, and a higher value indicates a higher structural similarity between images. SSIM serves as an assessment method for structural distortion according to the correlation between adjacent pixels. The SSIM results based on different models are summarized in Table 7.
After segmentation, the SSIM values of some images based on the DeepLabV3 + somewhat decrease, while those based on other models exhibit a similar tendency to the PSNRs, with the best performance observed in the PSP-M.
According to the three assessment indices, the PSP-M exhibits satisfactory segmentation performance, with clear image edges and excellent detail preservation. Therefore, it is suitable for ancient mural segmentation. In addition, our results also verify the feasibility of the application of deep separable networks in ancient mural segmentation.
Conclusions
Ancient Chinese murals are the crystals of the wisdom of Chinese working people, and they are one of the manifestations of Chinese civilization. Each mural possesses special historical and cultural backgrounds, and research on murals is a precious way for contemporary people to understand traditional culture. However, after a long history, these treasures, engraved on the wall, have been damaged to varying degrees, and a large number of exquisite murals are confronted with paint shedding, cracks in the bearing body and image defects, which affects information acquisition. Therefore, representing the content expressed in murals through technical means is a key issue in cultural relic protection, as well as a difficult task. The PSPNet network adopts the four-level pyramid module to extract the features of mural images, which reduces the loss of mural features. Furthermore, the adoption of the characteristic of deep separable convolution of MobileNetV2 may provide a new idea for mural image segmentation and improve the efficiency of ancient mural protection.
The combination of deep learning-based methods and models with ancient mural image segmentation serves as a new attempt at working methods for ancient mural protection. It is also a new manner of exploration in the related field. In this study, we combine a deep separable network structure and an image segmentation model with a satisfactory segmentation effect. This combination improves the segmentation accuracy and reduces the time consumption required by the model. The introduction of the Dice loss function into the model overcomes the negative influence on the segmentation effect caused by sample imbalance. Through a large number of comparative experiments, we verify the satisfactory applicability of deep separable networks in the field of mural segmentation.
However, some problems remain to be solved in the future. For instance, regardless of the model we use, loss of feature information seems unavoidable, and the application of various multiscale fusion networks could only restore the feature information as much as possible. For some images with sharp points, the feature restoration ability is poor, which constitutes one important reason why there is currently no universal model in the field of image segmentation. It is only through continuous attempts and explorations that great progress can be made to solve this problem.
Availability of data and materials
All data used for analysis in this study are included within the article and additional file 1.
Abbreviations
- PSP-M:
-
Pyramid scene parsing MobileNetV2 network
- FCM:
-
Fuzzy C-mean
- GMM:
-
Gaussian mixed model
- FCN:
-
Fully convolutional network
- SegNet:
-
Segment networks
References
Wang C, Pedrycz W, Li ZW, Zhou MC. Residual-driven fuzzy C-means clustering for image segmentation. IEEE/CAA J Automatica Sinica. 2021;8(04):876–89.
Wang C, Pedrycz W, Yang JB, Zhou MC, Li ZW. Wavelet frame-based fuzzy C-means clustering for segmenting images on graphs. IEEE Trans Cybern. 2019. https://doi.org/10.1109/TCYB.2019.2921779.
Wang C, Pedrycz W, Zhou MC, Li ZW. Sparse regularization-based fuzzy C-means clustering incorporating morphological grayscale reconstruction and wavelet frames. IEEE Trans Fuzzy Syst. 2020. https://doi.org/10.1109/tfuzz.2020.2985930.
Ashish KB, Arunangshu G, Immadisetty VK. A local contrast fusion based 3D Otsu algorithm for multilevel image segmentation. IEEE/CAA J Automatica Sinica. 2020;7(01):200–13.
Pare S, Kumar A, Bajaj V, Singh GK. A context sensitive multilevel thresholding using Swarm based algorithms. IEEE/CAA J Automatica Sinica. 2019;6(06):1471–86.
Park JH, Kang YJ. Evaluation index for sporty engine sound reflecting evaluators’ tastes, developed using K-means cluster analysis. Int J Automot Technol. 2020;21(6):1379–89. https://doi.org/10.1007/s12239-020-0130-8.
Qin XM, Li JL, Hu W, Yang JL. Machine learning K-means clustering algorithm for interpolative separable density fitting to accelerate hybrid functional calculations with numerical atomic orbitals. J Phys Chem A. 2020;124(48):10066–74. https://doi.org/10.1021/acs.jpca.0c06019.
Wang D, He K, Wang B, Liu XJ, Zhou JL. Solitary pulmonary nodule segmentation based on pyramid and improved grab cut. Comput Methods Progr Biomed. 2021. https://doi.org/10.1016/J.CMPB.2020.105910.
Song ZY, Ali S, Bouguila N. Background subtraction using infinite asymmetric Gaussian mixture models with simultaneous feature selection. IET Image Proc. 2020;14(11):2321–32. https://doi.org/10.1049/iet-ipr.2019.1029.
Liu KH, Ye ZH, Guo HY, et al. FISS GAN: A generative adversarial network for foggy image semantic segmentation. IEEE/CAA J Automatica Sinica. 2021;8(08):1428–39.
Iswanto IA, Choa TW, Li B. Object tracking based on meanshift and Particle-Kalman filter algorithm with multi features. Procedia Comput Sci. 2019;157(9):521–9. https://doi.org/10.1016/j.procs.2019.09.009.
Wu ZF, Shen CH, van den Hengel A. Wider or deeper: revisiting the ResNet model for visual recognition. Pattern Recogn. 2019;90(1):19–133. https://doi.org/10.1016/j.patcog.2019.01.006.
Sun QW, Chen W, Chao JG, Zhang HB. Flsnet: fast and light segmentation network. J Phys: Conf Ser. 2020;1518(1):12–47. https://doi.org/10.1088/1742-6596/1518/1/012047.
Chen C, Zhu YK, Papandreou G, Schroff F, Adam H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In: Proceedings of the European Conference on Computer Vision (ECCV), Cham, Springer, 2018, pp. 801–818. arxiv:1802.02611.
Chen C, Papandreou G, Kokkinos I, Murphy KL, Yuile A. DeepLab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. IEEE Trans Pattern Anal Mach Intell. 2018;40(4):834–48.
Francis NJ, Francis NJ, Francis NS, Axyonov SV, Aljasar SA, Xu Y, et al. Diagnostic of cystic fibrosis in lung computer tomographic images using image annotation and improved PSPNet modelling. J Phys Conf Ser. 2020;1611(1): 012062. https://doi.org/10.1088/1742-6596/1611/1/012062.
Oršić M, Šegvić S. Efficient semantic segmentation with pyramidal fusion. Pattern Recognit. 2020. https://doi.org/10.1016/j.patcog.2020.107611.
Chen LC, Collins MD, Zhu YK, Papandreou G, Zoph B, Schroff F, et al. Searching for efficient multi-Scale architectures for dense image prediction. NeurIPS 2018;9(11):arxiv:1809.04184.
Hu LD, Ge Q. Automatic facial expression recognition based on MobileNetV2 in Real. J Phys: Conf Ser. 2020;1549(2):21–36. https://doi.org/10.1088/1742-6596/1549/2/022136.
Huang Q, Sun JF, Ding H, Wang XD, Wang GZ. Robust liver vessel extraction using 3D U-Net with variant Dice loss function. Comput Biol Med. 2018;101(1):153–62. https://doi.org/10.1016/j.compbiomed.2018.08.018.
Stefano M, Quentin R, Matteo U, Claudio S. Causal dilated convolutional neural networks for automatic inspection of ultrasonic signals in non-destructive evaluation and structural health monitoring. Mech Syst Signal Process. 2021. https://doi.org/10.1016/J.YMSSP.2021.107748.
Yu F, Koltun V. Multi-Scale context aggregation by dilated convolutions.CoRR.2015. arxiv:1511.01722.
Howard AG, Zhu ML, Chen B, Kalenichenko D, Wang WJ, Weyand T, et al. MobileNets: efficient convolutional neural networks for mobile vision applications. Comput Vis Pattern Recognit. 2017;17(4):34–57.
Nan KM, Liu SC, Du JZ, Liu H. Deep model compression for mobile platforms: a survey. Tsinghua Sci Technol. 2019;24(06):677–769.
Anvar A, Cho YI. Automatic metallic surface defect detection using ShuffleDefectNet. J Korea Soc Comput Inform. 2020;25(3):19–26. https://doi.org/10.9708/jksci.2020.25.03.019.
Jiang JJ, Xiong YF, Xia X. A manual inspection of Defects4J bugs and its implications for automatic program repair. Sci China Inf Sci. 2019;62(10):31–46.
Xue F, Ji HB, Zhang WB. Mutual information guided 3D ResNet for self-supervised video representation learning. IET Image Proc. 2020;14(13):3066–75. https://doi.org/10.1049/iet-ipr.2020.0019.
Si YN, Pu JX, Zang SF. Neural network Q-learning algorithm based on residual gradient method. Comput Eng Appl. 2020;56(18):137–42. https://doi.org/10.3778/j.issn.1002-8331,1906-0175.(inChinese).
Tang W, Zou DS, Yang S, Shi J, Dan JP, Song GW. A two-stage approach for automatic liver segmentation with Faster R-CNN and DeepLab. Neural Comput Appl. 2020;32(1):1–10. https://doi.org/10.1007/s00521-019-04700-0.
Pan ZB, Tang J, Tardi T, Wu ZH, Xiao XM. A novel rapid method for viewshed computation on DEM through max-pooling and min-expected height. ISPRS Int J Geo Inf. 2020;9(11):633. https://doi.org/10.3390/ijgi9110633.
Lakshmi D, Thanaraj KP, Arunmozhi M. Convolutional neural network in the detection of lung carcinoma using transfer learning approach. Int J Imaging Syst Technol. 2020;30(2):445–54. https://doi.org/10.1002/ima.22394.
Shilpa S, Mamta K, Trilok K. Face mask detection using deep learning: an approach to reduce risk of coronavirus spread. J Biomed Inform. 2021. https://doi.org/10.1016/J.JBI.2021.103848 (prepublish).
Joshi K, Tripathi V, Bose C, Bhardwaj C. Robust sports image classification using InceptionV3 and neural networks-ScienceDirect. Procedia Comput Sci. 2020;167(3):2374–81. https://doi.org/10.1016/j.procs.2020.03.290.
Sterbentz RM, Haley KL, Island JO. Universal image segmentation for optical identification of 2D materials. Sci Rep. 2021;11(1):5808. https://doi.org/10.1038/S41598-021-85159-9.
Cao JF, Tian XD, Jia YM, Yan MM. Application of improved deeplab V3 + model in mural segmentation. Comput Appl. 2021;369(5):1471–6. https://doi.org/10.11772/j.issn.1001-9081.2020071101(inChinese).
Ren J, Gao L, Yu JL, Yuan L. Task scheduling strategy of energy efficient deep learning for edge devices. Chin J Comput. 2020;43(3):440–52. https://doi.org/10.11897/SP.J.1016.2020.00440 (in Chinese).
Xu ZY, Wang QC, Li D, Hu MH, Yao N, Zhai GT. Estimating departure time using thermal camera and heat traces tracking technique. Sensors. 2020. https://doi.org/10.3390/s20030782.
Shi WL, Du HQ, Mei WB. Novel channel attention residual network for single image super-resolution. J Beijing Instit Technol. 2020. https://doi.org/10.15918/j.jbit1004-0579.20022.
De Rosal S, Moses I. PSNR SSIM: imperceptibility quality assessment for image steganography. Multimedia Tools Appl. 2020;80(6):782. https://doi.org/10.1007/s11042-020-10035-z.
Acknowledgements
None.
Funding
This study was supported by the Key Research Base Project of Humanities and Social Sciences in Colleges and Universities of Shanxi Province (Grant No., 20190130).
Author information
Authors and Affiliations
Contributions
All authors contributed to the current work. JFC devised the study plan, led the writing of the article and supervised the entire process. XDT, ZQC, and LR conducted the experiments and collected the data, and YMJ performed the analyses.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Additional file 1.
Dataset.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated in a credit line to the data.
About this article
Cite this article
Cao, J., Tian, X., Chen, Z. et al. Ancient mural segmentation based on a deep separable convolution network. Herit Sci 10, 11 (2022). https://doi.org/10.1186/s40494-022-00644-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40494-022-00644-2
Keywords
This article is cited by
-
A Mamba based vision transformer for fine grained image segmentation of mural figures
npj Heritage Science (2025)
-
A damage detection network for ancient murals via multi-scale boundary and region feature fusion
npj Heritage Science (2025)
-
Delineating valuable content in Byzantine seals by combining deep learning and shape model of the border pattern
Multimedia Tools and Applications (2025)
-
A lightweight semantic segmentation algorithm integrating CA and ECA-Net modules
Optoelectronics Letters (2024)
-
Prediction of broken areas in murals based on MLP-fused long-range semantics
Heritage Science (2023)