An exploration of the self-similarity of traditional settlements: the case of Xiaoliangjiang Village in Jingxing, Hebei, China

Abstract

In order to retain the characteristics and style of traditional settlements and respect their layout and structure, it is necessary to carry out original planning and expansion of traditional settlements. This model of planning and expansion aims to protect the unique character of the settlement, maintain its original historical and cultural value, and integrate with the surrounding environment. Early research on the space complexity of settlements was dominated by qualitative analysis, and the depth of quantitative research on the spatial form of traditional settlements was insufficient. This article takes Xiaoliangjiang Village in Jingxing County, Shijiazhuang City, Hebei Province, which entered the fifth batch of the list of Chinese traditional villages list, as the research object. The spatial relationship of the settlement was obtained through field surveys and drone oblique photography, and the spatial morphological elements of Xiaoliangjiang Village were analyzed and extracted. Based on three quantitative theories of spatial form, namely topology theory, fractal theory, and space syntax, the self-similarity of settlements is analyzed from the perspectives of buildings, streets, and spaces. The research uses Matlab and DepthMap software to quantitatively analyze the spatial form of Xiaoliangjiang Village and obtains data. Through the analysis of data, it was found that Xiaoliangjiang Village has self-similarity at three levels: buildings, roads and settlement spaces. The buildings iteratively generate various forms of architectural courtyards through the basic “L”-shaped pattern. The spatial structures at all levels of roads and settlement space in Xiaoliangjiang Village are relatively similar, in line with the bottom-up traditional settlement evolutionary law. By studying settlement self-similarity, people can better understand the formation mechanism of traditional settlement space structure and its evolution law. At the same time, it enriches the research perspective of traditional settlements and provides technical support for analyzing the self-similarity of traditional settlements and settlement protection planning.

Introduction

Background

Traditional settlements are an important part of cultural heritage in China, with rich cultural connotations and unique spatial characteristics. Its connotation includes rich social relations, traditional customs, architectural art and traditional industries. The spatial components mainly include geographical environment, building layout and road traffic. The spatial structure usually presents the characteristics of being surrounded by a center, well-proportioned, and dense distribution. The evolution of traditional settlements is affected by many factors such as history, geography, economy and culture, and presents a dynamic balance between protection and development, inheritance and innovation.

With the acceleration of urbanization and population migration to cities, traditional settlements are facing a crisis due to the lack of vitality and vigor. At the same time, population reduction also leads to the lack of maintenance and repair of buildings, and the spatial form and living environment of the settlement is facing serious challenges [1].

The spatial form of a settlement is influenced by local culture, but under contemporary rapid development and construction, there is generally a lack of understanding of the cultural connotations of traditional settlements. Urban-like planning has undermined the original bottom-up evolution of these settlements, making it difficult to follow their historical development during the conservation planning and expansion of these settlements. Excessive commercial development and uniform construction patterns have plunged the development and construction of traditional settlements into the predicament of “Many villages have the same appearance”. The problem of homogenization of traditional settlements is serious, and their unique regional characteristics are gradually disappearing. From the viewpoint of the current protection and development of traditional settlements, there is a general lack of in-depth excavation and refinement of the characteristics of their space patterns and a lack of systematic research on local spatial form factors.

Meanwhile, in past studies, the morphology of traditional settlements mainly relied on qualitative analysis [2, 3], which could provide rich historical and cultural information but did not dig deeper into their space morphological characteristics and formation laws. The quantitative research methods developed later offer more data and statistical information for studying traditional settlements [4, 5]. However, previous quantitative research methods have made it challenging to address the issue of planning and expansion while continuing the settlement’s unique style. This is because traditional settlements often have unique spatial layouts, architectural styles, and social structures. It is difficult for traditional quantitative methods to capture these complex features accurately.

With the implementation of the rural revitalization strategy, the protection and study of traditional settlements have become increasingly important. The spatial form of traditional settlements is a complex system formed by various factors, and studying its spatial form is crucial for protecting and developing traditional settlements. Traditional settlements are the fruit of the collective wisdom of the ancestors over the generations, and they are dynamic evolutionary systems that contain profound historical and cultural deposits. The spatial form, as the outward expression of traditional settlement culture, includes the wisdom and thoughts of the ancients. The architecture, layout, and traditional lifestyle of the settlement reflect the social structure and development process in the past and have significant research value. At the same time, many traditional settlements attract tourists because of their unique culture. Through research and conservation, people can develop these settlements into cultural tourism destinations. This will not only bring new opportunities for the local economy but also encourage people to pay more attention to and understand the local traditional culture.

Research objective

In summary, previous studies lack analytical methods suitable for protecting the uniqueness of settlements and conducting original planning and expansion of spatial forms in traditional settlements. Therefore, in this study, our goal is to explore the original planning and expansion of traditional settlements to balance the needs of improving residents’ living quality and protecting the original spatial form of settlements. We will focus on how to improve infrastructure and expand new living space while respecting the traditional architectural style and layout structure to ensure that the new part is in harmony with the original settlement space structure and architectural style. Through such planning and expansion, it can not only meet the living needs of residents, but also protect and inherit the cultural heritage of settlements. At the same time, tourists can better experience the original cultural atmosphere and spatial characteristics of the settlements, thereby promoting the development of local tourism, boosting the prosperity of related industries, and increasing local economic income.

Therefore, our main objective is to analyze the settlement layout and morphology by studying settlement self-similarity (self-similarity means that objects or systems have similar structures or forms at different scales. Traditional settlements are often built according to a particular order and pattern, and this self-built order may have similar structures at different scales). In this way, the intrinsic structural and layout characteristics can be better understood, and repetitive patterns of layout and structural regularities in the settlements can be discovered in order to guide the development and planning of the settlements. In order to solve this problem, topological theory, space syntax, and fractal theory have been introduced into the study of traditional settlements. These three theories can intuitively reveal the self-similar characteristics embedded in the settlement space and provide a basis for settlement planning and design. Meanwhile, these theories can also verify the rationality and effectiveness of traditional settlement planning and expansion.

Relevant concepts and grounded theory

Self-similarity

Self-similarity refers to a particular structure or process of a system or object of study that has similarities at different space scales or time scales or that also has specific similar properties in the whole and parts of the system, in the whole and in the whole, and in the parts and in the parts [6].

The study of self-similarity can be traced back to 1967 when French mathematician Benoit Mandelbrot proposed the concept of “self-similarity” in his article “How Long Is the Coast of Britain?”. The coastline exhibits a similar geometric structure at all scales, providing a preliminary study of the self-similarity phenomenon [7]. Since then, the concept of self-similarity has been used in a wide variety of fields, including geology, biology, and computer science. In geology, self-similarity can be used to describe some natural phenomena, such as river networks and mountain landscapes [8,9,10]. In biology, self-similarity can be used to describe the structure and morphology of living organisms. For example, fractal geometry is used to study the branching structure of trees and the structure of the human brain [11, 12]. In computer science, self-similarity is used in fields such as image processing, image compression, and Internet traffic analysis [13,14,15,16].

Cities are typical man-made living environments with specific characteristics of self-similarity. The self-similarity theory was earlier applied more to the study of urban space. Batty and Longley discussed the application of self-similarity in urban planning. The authors proposed the concept of “fractal city”, described the self-similarity characteristics of urban space structure [17], and applied self-similarity and fractal theory to explain the space structure and development patterns of cities [18]. Allen developed the concept of cities and regions as self-organizing systems, which covers topics such as self-similarity and complexity and examines the self-similar characteristics of urban and regional systems [19]. At the same time, other elements of the city were also studied. For example, Jia Bing calculated the fractal dimension value of the city skyline through the Matlab platform. She elaborated on the impact of self-similarity on the integration of skyline levels, the orderliness of architectural textures, and the completeness of road networks, as well as some of people’s perceptions and experiences of these three [20].

Self-similarity theory has also been studied about transportation networks. The regularity and self-similarity of road systems were revealed through fractal analysis of transportation networks [21, 22]. On this basis, the network coverage pattern model of fractal theory was applied to analyze and calculate the coverage pattern of transportation networks. The similarity between the new network and the original network was reflected by calculating the fractal dimension values under different road coverage patterns [23]. With the deepening of research, it has been found that urban road networks exhibit a hierarchical structure. This is due to the existence of a road network hierarchy, and each level has similar structural characteristics, which reflect the road network’s similarity. Meanwhile, the fractal structure and self-similar structure in the road network helped improve the efficiency of traffic transmission in the system [24]. Subsequently, the GIS platform has been gradually introduced to study the fractal dimension of the road network. By analyzing the urban road network through fractal theory on the GIS platform, the similarity dimensions of different levels were measured [25].

There are also some studies on traditional settlements. For example, the self-similarity among farmland, settlements, and forests was analyzed by studying the capacity fractal dimension [26]. Subsequently, the analysis of self-similarity was extended to settlement façades. The self-similarity and complexity of traditional settlement facades were quantitatively analyzed by the box-counting method [27]. There are also researchers who have combined the box-counting method with Grasshopper programming calculations to illustrate the degree of self-similarity in the spatial forms of settlements by comparing the fractal dimension values of different levels [28]. In terms of categories, most studies on self-similarity have focused on the spatial structure of cities and road networks in cities, however, there are fewer studies on the self-similarity of traditional settlements. Meanwhile, most studies on self-similarity are based on fractal theory. Most of the researches study the complexity of each scale level of the settlement through the fractal theory, and the researches about the self-similarity of the settlement are less involved and do not analyze the self-similarity embedded in the settlement from multiple aspects. To address this gap, this study focuses on self-similarity in traditional settlements and analyzes it at three levels: architecture, street and space. This multifaceted research approach not only fills the previous gap, but also provides us with a more comprehensive and complete perspective to explore the connotation and characteristics of self-similarity in traditional settlements in greater depth.

Topological theory

Topology is the study of geometric figures or spaces in which some properties remain unchanged after successive changes in shape. It only considers the positional relationship between objects without considering their shapes and sizes. Topology simplifies and abstracts space into points and lines, which are used to construct topological networks [29]. The theory is widely used in urban planning, village planning, architecture, and other fields [30,31,32]. By using the principles of topology to simplify the layout of the settlement’s architectural courtyards, it is possible to visualize more intuitively the self-similarity that exists in the architectural arrangement.

Fractal theory

The fractal theory is a geometric discipline that describes nature and was first introduced by mathematician Benoit Mandelbrot in the 1970s [33]. Fractal means irregularity, fragmentation, etc., and its most essential feature is the study and analysis of complex fractal geometries using fractal dimension [34]. Fractals are structures composed of repeating patterns that can be seen as similar shapes on both large and small scales, i.e., a fractal is a geometric shape or figure that is self-similar on all scales [35].

Fractal dimensions can be calculated using different methods; one of the most commonly used methods is the box-counting method. The box-counting method is a calculation method that measures the dimension of a fractal in space. To calculate the dimensionality of a fractal, place the fractal figure on a uniformly divided box grid and count the number of grids occupied by this fractal figure. The fractal dimension value is calculated by progressively refining the grid to see the change in the number of grids covered [36, 37].

Space syntax

Space syntax was born in the late 1970s. It was first proposed by Bill Hillier, a professor at the University of London in England, and others as a theory and research method for quantifying spatial forms. It was later used by architects to study the impact of architecture and urban space layout on human activities, socioeconomics, and the environment [38]. There are more achievements in applying the space syntax method to the study of the space morphology of traditional settlements, which are mainly related to the planning of settlements, residential remodeling, space structure, etc. [39].

Intelligibility is one of the concepts in space syntax. Intelligibility is used to describe the degree of correlation between a local space and the overall space, or to measure the degree of understanding of the entire space system through the local space [40].

Study area

Xiaoliangjiang Village is located in Nanzhangcheng Town, Jingxing County, Shijiazhuang, Hebei Province, in the hinterland of Taihang Mountains at the junction of Hebei and Shanxi. The village has a large number of architectural courtyards built in Ming and Qing dynasties, which are well preserved. Liang Min, the ancestor of the Liang family, moved here from Xicheng Village in Pingding, Shanxi Province. The village was originally named Xiaoliangjia. In 1877, a mountain torrent carved a 20-km-long trench here, which was regarded as a river locally. Then Xiaoliangjia was renamed Xiaoliangjiang, and the current layout of the village began.

Xiaoliangjiang Village has a unique geographical environment, surrounded by mountains on all sides, like a mountain basin. The site is high in the north and low in the south, and is built along the side of the road and against the mountain. The older areas in Xiaoliangjiang Village are distributed in a cluster, and the new village is located on the east side of the old village and is distributed in a strip, as shown in Fig. 1. The emergence of new villages is to adapt to modern people’s lives and make up for the shortcomings of old villages. The existence of new villages has played a role in protecting ancient villages to a certain extent. In addition to the ancient building complexes, Xiaoliangjiang Village also preserves ancient temples, ancestral halls, and theaters, all of which have a long history and distinctive local characteristics. The Stage in Xiaoliangjiang Village is gathered together with the sacrificial buildings “Wudao Temple”, “Zhenwuge” and “Longwangtang”, and is an important public activity space for the villagers. Ancestral halls are built at important transportation hubs and populated areas of the settlement, becoming the center for villagers to gather and communicate. The Stage is an important cultural and entertainment place for villagers, and therefore creates a certain agglomeration effect. These public buildings are not only the landmark buildings of the settlement, but also an important part of the villagers’ life, shaping the unique spatial characteristics and community culture of the settlement.

Fig. 1

Xiaoliangjiang village texture map

Xiaoliangjiang Village has simple folkways and customs near ancient time. Various types of stone utensils can be seen everywhere, which has become a landscape of this ancient village. The architectural form of the residential buildings is mostly courtyard architecture. The architectural design emphasizes environmental coordination and functional zoning, with living areas, storage areas, kitchens, and other functions clearly defined. The building materials are all soil, wood and stone structures. The older buildings in the settlement have pitched roofs, while the rest have flat roofs. Flat-roofed houses are simple in structure and low in cost, and are generally built for small families who are not financially well-off. At the same time, the flat roof can be used to dry crops such as grain. The villagers of Xiaoliangjiang choose a location to build their houses based on the actual local topography. They usually choose a sunny and bright location based on the mountainous terrain. The main industry in the village is planting. The main crops are corn, and fruit cultivation mainly focuses on walnuts, persimmons, and apples.

Xiaoliangjiang Village, with its long history and deep cultural heritage, is one of the cultural tourist attractions characterized by Jin culture and has been included in the fifth list of Chinese traditional villages in recent years. However, with the gradual progress of urbanization, some problems have arisen in Xiaoliangjiang Village. The lack of population and the aging of the population have led to the deterioration of the buildings (Figs. 2, 3) and the deterioration of the living environment of the villagers. The internal space of the settlement is very confined, with less space for public activities, and the elderly living here lacking space for daily activities.

Fig. 2

Partial building plan of Xiaoliangjiang Village

Fig. 3

Partial building plan of Xiaoliangjiang Village

Methods

Data sources

The data in this article was obtained from field research. The top-view image of the settlement was captured by the Unmanned Aerial Vehicle tilt photography technique, and then the photo was imported into ContextCapture to build a model (Fig. 4). With reference to the generated model, a detailed map of the settlement texture and road network was drawn in AutoCAD.

Fig. 4

Model view of Xiaoliangjiang Village

Research methodology

The main steps of this study are shown in Fig. 5. Firstly, the settlement model is established using the UAV tilt photography technique. Then, the road map and texture map of the settlement are drawn according to the established model. Secondly, topology theory is used to analyze the self-similarity of the buildings in the settlement; the box-counting method is used to measure the fractal dimension values of the roads at different levels and analyze their self-similarity; the box-counting method and intelligibility are used to analyze the self-similarity of the space of the settlement, and a comparative analysis is made between the two methods. Finally, the self-similarity of the settlement is analyzed in a comprehensive way by integrating the three levels of buildings, roads, and spaces.

Fig. 5

Technical route

Pointed self-similarity features—architecture

Analyzing architectural self-similarity is done using a topology-theoretic approach. Using the principles of topology, a building can be regarded as a node of one, and for a building such as a traditional residential building, its architectural distribution can be regarded as a matrix of points on a two-dimensional plane. In this array of points, neighboring buildings are connected by lines. By analyzing the relationship between lines and nodes, information about the distribution of architectural space within the courtyard can be learned. The diagram that describes the structural relationship through nodes and connecting lines is called the relationship diagram [31]. This topological relationship diagram provides an effective description of the space configuration, which in turn can analyze the self-similarity embedded in the architectural arrangement of traditional residential buildings.

When establishing the topological relationship of a residential courtyard, firstly, the shape and size factors of traditional residential buildings are removed, and it is regarded as a point element with positional information. Then, the neighboring residential buildings are connected by lines, and finally, the graph with only lines and nodes is obtained. By collecting different forms of layout diagrams of residential buildings, and then translating their layout forms, different diagrams of topological relationships are obtained, and then analyzed.

By analyzing the topological relationship diagrams of different traditional residential buildings, it is possible to show more intuitively the pattern of building arrangement in them and then analyze the self-similarity shown in them. By analyzing the architectural arrangement of some traditional courtyards, it can be seen that there are repeated basic structural units in the courtyards. For example, some small traditional courtyards may have only two or three rooms and an enclosing wall, while in large palaces, there may be hundreds or even thousands of rooms and enclosing walls. But regardless of size, there are basic structural units that are all reused and take on the same or similar forms.

Linear self-similar features—roads

Whether it is a square grid-type road network structure, a ring-radial road network structure, or a free-form road network structure, in order to ensure the integrity and balance of the overall structure, there exists a self-similarity in morphology between the road network structures of each level and with the overall road network structure [20]. In fractal theory, the parameter that describes the self-similarity between the drawing localization and the whole is the dimension in the fractal sense. Here, the box-counting method is used to calculate the fractal dimension of each level of the settlement road and analyze its self-similarity. Small square boxes with side length r are taken to cover the analyzed area, where the square boxes with roads passing through them are set as non-empty boxes, and the number of non-empty boxes is set as N(r). Change the value of side length r to get its corresponding number of non-empty boxes N(r). Finally, apply the least squares method in double logarithmic coordinates to fit the resulting series of r and N(r) to a straight line, and the slope of the resulting straight line is the required fractal dimension. The formula for calculating the fractal dimension value is as follows:

$${\text{D}}_{b} = \frac{{{\text{log}}N_{n + 1} - {\text{log}}N_{n} }}{{{\text{log}}\left( {1/r_{n + 1} } \right) - {\text{log}}\left( {1/r_{n} } \right)}}.$$

The plan view of the settlement road was imported into Matlab software for binarization to obtain a black-and-white monochrome picture, after which it was imported into Matlab for fractal calculation.

The settlement road network is a typical fractal, and the distributional characteristics of settlement roads can be evaluated with the help of fractal theory. The self-similarity in fractals can be self-similar in an absolute sense or self-similar in a statistical sense. The latter is the theoretical basis for studying the self-similarity of the settlement road network, i.e., the self-similarity theory in the statistical sense [41].

By calculating the number of fractal dimension values, it is possible to understand whether the structural characteristics of the road network remain similar at different scales. The physical significance of the fractal dimension number expression is now illustrated by the following figure (Fig. 6). Take a square with side length R. Inside this square, assume there is a road passing through it. When we further divide this square into four smaller squares of side length R/2, the following four cases occur [23, 42].

• 1. When a road passes through each of these four small squares, the computation yields the dimension value D = 2. The new network has exactly the same structural characteristics of the roads compared to the original network.

• 2. When there are roads passing through three of the small squares, the dimension value D = 1.58946 can be obtained by calculation. The new network still has a similar morphology compared to the original network, but not exactly.

• 3. When two of the small squares have roads passing through them, the dimension value can be calculated to be D = 1. The self-similarity of the road network is low, and the new network has a large change in morphology compared to the original network.

• 4. When there is only one small square with a road passing through it, the fractal dimension value is calculated to be D = 0. This indicates that the self-similarity of the road network is very low, and the new network has a very large change in morphology compared to the original network. Therefore, the interval of the fractal dimension values is 0 ≤ D ≤ 2. When the number of fractal dimension values is close to 2, it indicates that the road network has complete self-similarity because, at this point, the situation before and after the subdivision of the square is completely similar, and there is a road passing through each square. The closer the number of fractal dimension values converges to 2, the higher the self-similarity of the road network [23]. In summary, the box-counting method can be used as an effective means to quantify the degree of self-similarity of transportation road networks.

Fig. 6

Fractal dimension values of roadways under different coverage scenarios

Faceted self-similarity characterization—space

Self-similarity is reflected in the spatial distribution of some traditional settlements. From the smallest building units to the single units through a certain combination of arrangements to form a courtyard. From the formation of a single courtyard to several courtyards to form a neighborhood group. From a local neighborhood group to the entire settlement. They have a certain number of nested patterns at different observation scales, reflecting the self-similarity between different observation scales. At the same time, there is also some self-similarity between the same scale levels [43].

• 1. Research methodology—box-counting method

  Because of the need to analyze the different scale spaces, the box-counting method with high applicability is used for the calculation and analysis of fractal dimensions. The specific algorithm is the same as the box-counting method for computing lines mentioned earlier. As r changes, the value of N(r) also changes. The smaller the box side length r is, the larger N(r) is, and vice versa. Finally, the resulting series of r and N(r) are fitted to a straight line in double logarithmic coordinates using the least squares method, and the slope of the resulting straight line is the desired fractal dimension. The correlation coefficient between the straight line and the column of points is R², and the higher the value of R², the more obvious the self-similarity characteristic of the research object. Generally R² ≥ 0.996, we consider it to be characterized by self-similarity within the calculated scale interval. The formula for calculating the fractal dimension value is as follows:

  $${\text{D}}_{b} = \frac{{{\text{log}}N_{n + 1} - {\text{log}}N_{n} }}{{{\text{log}}\left( {1/r_{n + 1} } \right) - {\text{log}}\left( {1/r_{n} } \right)}}.$$

  The box-counting method is a common method to calculate the fractal dimension, which can reflect the degree of self-similarity and complexity of fractals. The texture map of the settlement is imported into Matlab software for binarization to obtain black and white monochrome pictures, and then the fractal is calculated in Matlab.

  When calculating the fractal dimension of a plane, most of the theoretical values of the fractal dimension values are in the range [1.0, 2.0] [44]. 1.0 represents the shape of the simplest square graphical patches, while 2.0 represents the most complex graphical patches. In the calculation of fractal dimensions, the quantitative analysis of dimensions can analyze the complexity and degree of self-similarity of the development of traditional settlement spatial form. In fractal theory, the box-counting method can be used to measure the fractal dimension values of different levels of the settlement space. By comparing the size of the fractal dimension values of different levels, the self-similarity of the settlement space can be intuitively reflected.

  If the fractal dimension values of each level of settlement space are very similar, it means that the process of evolution and development of settlement space is hardly influenced by other factors. The complexity and continuity of each level of the settlement are good, and the degree of self-similarity of the settlement space is very high [28].

  If the fractal dimension values of the different levels of the settlement space show a trend of gradual decrease or gradual increase in a small range and the difference in the fractal dimension values between different levels is small, it means that the settlement space has gradually become simpler or more complex under the action of some environmental factors. This implies that the settlement has a similar space distribution pattern on different scales, and the degree of self-similarity of the settlement space is high [28].

  If the fractal dimension values at each level of the settlement space differ greatly and there is a significant difference in the fractal dimension values between certain two levels, it means that the settlement space is subjected to many influences from the external environment. This implies that the space distribution patterns of settlement at different scales are very different, and the degree of self-similarity of the settlement space is low [28].

• 2. Research methodology—intelligibility

  Intelligibility is the study of the relationship between the local and the whole, which has some similarity with the self-similarity theory that studies the relationship between the local and the whole of the system. Therefore, we measure intelligibility. If the results are similar, it is possible that intelligibility can reflect the degree of self-similarity of the settlement. If the results are contrary, then it must not be used to reflect the self-similarity.

  In DepthMap software, a linear regression analysis is done on the global integration of the settlement and the local integration of the settlement with a topological step of 3. Then the correlation coefficients of the scatter plot are derived by means of mathematical analysis, and the intelligibility of the space can be obtained.

  The horizontal coordinate is the “global integration degree” and the vertical coordinate is the “local integration degree”, and the formula is as follows.

  $$R^{2} = \frac{{\left[ {\sum\nolimits_{i = 1}^{n} {\left( {I_{i} - \overline{I}} \right)\left( {{I_{i}}^{\prime } - \overline{I}^{\prime}} \right)} } \right]^{2} }}{{\sum\nolimits_{i = 1}^{n} {\left( {I_{i} - \overline{I}} \right)^{2} \sum\nolimits_{i = 1}^{n} {\left( {{I_{i}}^{\prime } - \overline{I}^{\prime}} \right)^{2} } } }},$$

  where $I_{{\text{i}}}$ is the local integration degree value of node i; $\overline{I}$ is the average value of local integration; ${I_{i}}^{\prime}$ is the global integration value of node i; $\overline{I}^{\prime}$ is the global integration average.

  According to the theory of space syntax, the value of intelligibility is generally controlled between 0 and 1. The definition of the strength of correlation, i.e., goodness of fit, in mathematical analysis is followed here. When 0.0 < R² ≤ 0.5, the local integration degree is weakly correlated with the global integration degree. When 0.5 < R² ≤ 0.7, the correlation between local and global integration is average. When 0.7 < R² ≤ 1.0, the correlation between local and global integration is strong. The range of R² values is used to determine the strength for intelligible [45]. When the value is greater than 0.5, it represents a higher degree of space intelligibility. People have a higher level of perception of global space when they are in local space, and the distribution of space is regular and easy to recognize. When the value is less than 0.5, it represents a lower level of space intelligibility. The space is less readable and less recognizable.

  Construct the space axial map of the settlement in CAD, save it as a “.dxf” format file recognizable by the software DepthMap, and then import it into DepthMap software to calculate the global integration value and local integration value. Combining both sets of data generates the scatterplot. The two sets of data, global integration, and local integration, were selected for regression linear analysis in the software. The X-axis represents the connection values, the Y-axis represents global integration, and the R² represents the degree of intelligibility.

Comparison of the two methods

There are various methods that can be used to analyze the fractal dimension values of settlement streets and spaces; for example, the methods for measuring streets are the box-counting dimension, length dimension, branching dimension, and correlation dimension. Methods for measuring space include the box dimension method and the area perimeter method. However, in order to highlight the difference between the local and the whole, we use the box-counting dimension method, which can analyze different scales, to measure the fractal dimension values of roads and spaces so as to analyze the relationship between the local and the whole at different scale levels.

To analyze the self-similarity of space, the relationship between the local and the whole is analyzed. In the box-counting method, there are measurements and comparisons between small and large scales. There is also a comparative analysis between local integration and global integration in intelligibility. However, both of them have the same points and have different point.

Same point:

• 1. Both are concerned with structure and organization: both the box-counting method and intelligibility focus on the structure and organization of the research object or space, trying to reveal its regularity and characteristics.

• 2. Both use mathematical models: both use mathematical models to describe and understand the characteristics and properties of the object or space under study.

• 3. Fields and applications: both can be applied in the fields of urban planning, architectural design, and transportation planning to study the influence of space structure on human behavior and interaction. The box-counting method is also used in the field of natural science and mathematics to study complex systems and self-similarity in nature.

Points of difference:

• 1. Distance considerations: when analyzing fractal patterns, the box-counting dimension method usually takes into account actual physical distances. Fractal theory is concerned with the self-similarity and complexity of graphs or spaces, where distances usually refer to physical distances in real space. The box-counting method reveals the self-similarity of a graph by measuring and calculating its dimensional and structural characteristics at different scales.

  In intelligibility, the notion of distance is usually based on topological distance, i.e., considering space-to-space connectivity relationships rather than actual physical distances. Space syntax is concerned with the effects of Space structure and layout on human behavior and interaction, where distance usually refers to topological connectivity relationships between objects, such as connectivity analysis between nodes in a road network. This reflects the differences in research methodology between the two theoretical frameworks to suit the needs of their respective research areas and problems.

• 2. The way to study the relationship between the local and the whole: both the box-counting dimension method and the intelligibility are concerned with the relationship between the local and the whole in a settlement. However, the box-counting dimension method analyzes the relationship between the local and the whole by studying different scale levels. Intelligibility, on the other hand, analyzes the relationship between the local and the whole by comparing different topological distances.

• 3. Objectives and applications: the objective of the box-counting method is to study and characterize the local-whole relationship of fractal structures in nature, thus revealing their complexity and self-similarity. Intelligibility aims to assess the intelligibility and navigability of settlements in order to optimize urban planning and architectural design and to improve human understanding and perception of settlement structures.

  To summarize, the box-counting dimension method of fractal theory and the intelligibility of space syntax has some similarities and differences in terms of the relationship between the local and the whole in the study of settlements. Although both focus on the relationship between parts and the whole, there are differences in the methods of considering distance, the ways of studying the relationship between parts and the whole, and their goals and applications.

Results

Pointwise self-similarity feature

This study focused on the residential architecture in Xiaoliangjiang Village, where a survey was conducted to obtain the residential plan of the traditional settlement. After that, we made a selection of residential courtyards and extracted some typical residential courtyards. The main courtyard forms in Xiaoliangjiang Village are as follows:

• (1) Enclosed on two sides

  The double-sided enclosed courtyard has lower cost and smaller area. It is built against the mountain and faces south, making it more flexible in terms of space adaptability. Although small in size, it is fully functional. Buildings with double-sided enclosed courtyards are generally located on the north and west sides or on the north and east sides. The houses on the north side are the main houses, arranged in a straight line, and are mostly bedrooms for a family. There are secondary rooms on the east or west side, which are mostly storage spaces. They can also be used as wing rooms for families with a larger population. Xiaoliangjiang Village has a large terrain difference, and the courtyard organization form is mostly affected by the land plot. Villagers generally choose a relatively open place to build a double-enclosed courtyard, and then choose the location of the building according to their needs.

• (2) Enclosed on three sides

  There are many courtyards enclosed on three sides in Xiaoliangjiang Village. The courtyards enclosed on three sides have a higher sense of spatial enclosure and give people a sense of security in space. Most of the courtyard buildings enclosed on three sides are mainly distributed on the north and east and west sides, and their form is similar to that of a typical courtyard house. In most cases, the house on the north side is the center of the entire courtyard, and wing rooms are set up on the east and west sides to make up for the functional deficiencies of the central house. The enclosed courtyard is used for drying grain and various crops. Most of the families with courtyards enclosed on three sides are in a fair financial situation and their courtyards are well protected.

• (3) Enclosed on four sides

  Enclosed on four sides is the most typical courtyard form in Taihang Mountain, which is a relatively closed courtyard form. There are thick stone walls around the courtyard, and the internal buildings are arranged along an axis, with auxiliary buildings built on both sides of the main axis building. The courtyard enclosed on four sides was built in strict accordance with the ancient patriarchal system. The courtyard should not only meet the functional requirements, but also reflect the spiritual functions of being orderly in terms of age and hierarchy. The house on the north side is the owner’s residence, the east and west wings are rooms for the juniors, and the south side is the back room. The courtyards enclosed on four sides in Xiaoliangjiang Village have high artistic attainments and have great research value.

  When establishing the topological relationship of the residential architecture in Xiaoliangjiang Village, firstly, it is necessary to translate the architectural elements and wall elements of different types of residential courtyards in the settlement into multiple different topological relationship diagrams, as shown in Table 1.

  Analysis of the table reveals that the basic courtyard layout in Xiaoliangjiang Village is composed of two nodes and one line, forming an “L”-shaped basic unit structure. Based on this unit structure, a “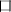”-shaped layout structure is formed through central symmetry, which corresponds to the layout of the courtyard surrounded by four sides in the settlement. In addition, new layout structures can be generated through axial symmetry. Through axial symmetry, a “∏”-shaped layout structure is generated, which corresponds to the layout of the courtyard enclosed on three sides in the settlement. By symmetrically transforming these basic layout structures vertically or horizontally, there are some new layout structures were created, which correspond to some layouts in the settlement. The design of the courtyard can be further enriched in the settlement by this method.

Table 1 Courtyard relationship diagram

Linear self-similar features

Extracting the road texture of Xiaoliangjiang Village for analysis. Firstly, we need to determine the scale level for analysis. Unlike in urban contexts, when the study object is a village settlement, the selected scale level is relatively small due to the smaller study area and lower road level. The selected scale is 12.5 m, 25 m, 50 m, and 100 m, which corresponds to the three observation scales of entrance roads, intra-cluster roads and inter-cluster roads, which facilitates interpretation and analysis [46]. Secondly, the box-counting dimension of the road network in Xiaoliangjiang Village was measured by Matlab, and the double logarithmic curve was plotted. The calculation results are shown in Fig. 7.

Fig. 7

Calculation of fractal dimension values of settlement roads

The overall fractal dimension of the road network in Xiaoliangjiang Village is calculated to be 1.499. Generally, a fractal dimension value of 1.4 or more indicates that the road network has good spatial coverage, with a network-like form structure. The fractal dimension value above 1.2 indicates that the road network has average spatial coverage, with roads in the form of a tree-like branching structure. A fractal dimension value below 1.2 indicates that the road network has weak space coverage ability and no obvious morphological structure [46]. It can be seen that the road network in Xiaoliangjiang Village is dominated by a network-like morphological structure. The higher fractal dimension value of the road network, the better space coverage ability, accessibility and connectivity of the roads, and the self-similarity of the road network of the settlement are also at a high level.

Through fractal calculation of the roads in Xiaoliangjiang Village, the correlation R² of the fractal result of the roads is 0.9965, passing the correlation test (R² ≥ 0.996). Moreover, the overall fractal dimension value of the road is relatively high, and the fractal dimension value is close to D = 1.589. There are relatively high similar shapes between the various levels of the road. This shows that the road network in Xiaoliangjiang Village has a certain degree of self-similarity. The fractal dimension values of the roads in Xiaoliangjiang Village at 12.5–25 m, 25–50 m, and 50–100 m scales are 1.265, 1.558, and 1.654, respectively. The tree-like branching structure of the road network is more evident at small-scale scales such as entrance roads. In terms of medium and large scale scales such as intra-cluster roads and inter-cluster roads, the network-like branching characteristics are also clearly reflected. The scale with the lowest fractal dimension value of settlement roads is the 12.5–25 m interval. The lower fractal dimension values of the roads at this scale indicate a larger gap between the structural forms of the roads in those two levels with a low degree of self-similarity between them. The scale with the highest fractal dimension value of the roads in the settlement is the 50–100 m interval. The higher fractal dimension value of roads at this interval indicates that there is not much difference in the structural forms of roads at these two levels, with a high degree of self-similarity between them. Based on the above analysis data, the fractal dimension value of the settlement road network in Xiaoliangjiang Village falls within the range of fractal dimension values of settlement road networks in self-organized environments, indicating a certain degree of self-similarity in the settlement road network.

Facial self-similarity features

Self-similar features based on box-counting dimension

The first step is to select the appropriate scale levels. 100 m can see the changes in building form, and 20–30 m can see the changes in building details. Considering the overall scale of Xiaoliangjiang Village, the scale levels adopted in this article are 100 m, 50 m, 25 m, and 12.5 m. The box-counting dimension values of the texture map of Xiaoliangjiang Village were measured by Matlab software, and the results are shown in Fig. 8. The fractal dimension values for each scale level are as follows: for the 50–100 m scale, the fractal dimension value is 1.512; for the 25–50 m scale, it is 1.658; for the 12.5–25 m scale, it is 1.719. The overall fractal dimension of Xiaoliangjiang Village is calculated to be 1.632.

Fig. 8

Calculation of the fractal dimension values of the settlement space

The correlation R² of the fractal results is 0.9992, passing the correlation test (R² ≥ 0.996). This shows that the settlement space of Xiaoliangjiang Village has a certain degree of self-similarity. The theoretical values of the fractal dimension values are between 1.0 and 2.0, with 1.0 representing the simplest square graphical patches and 2.0 representing the most complex graphical patches. Less than 1.3794 belongs to the low fractal dimension region, more than 1.5046 belongs to the high fractal dimension region, and in between belongs to the medium fractal dimension region [47]. From the above calculations, it can be seen that the fractal dimension value of Xiaoliangjiang Village is in the high fractal dimension value area, and its fractal dimension value of each level fluctuates in the higher value range. The difference between the maximum and minimum values of the fractal dimension values is 0.207, and the difference between the fractal dimension values of each level is not large and within a reasonable range. Based on the analysis data, the fractal dimension value of the settlement space in Xiaoliangjiang Village falls within the range of dimension values of settlement spaces under self-organized environments. The settlement spatial form exhibits a certain degree of self-similarity, and the settlement space of Xiaoliangjiang Village demonstrates the characteristic of “bottom-up” natural fractals under the influence of mountainous environmental factors.

Self-similar features based on intelligibility

In Depthmap software, linear regression analysis was conducted on the global integration degree of Xiaoliangjiang Village and the local integration degree of topological step 3. The results of the analysis are depicted in Fig. 9. The abscissa in the figure is the degree of local integration, the ordinate is the degree of global integration, and R² is the degree of intelligibility. From the red point in the upper right corner to the purple point in the lower left corner, the degree of integration is represented from high to low, and the black line in the middle is the fitting straight line.

Fig. 9

Results of intelligibility calculations for settlement

The farther the colored points are from the scatter of the fitted straight line, the lower the intelligibility. This is because the farther the points are from the fitted straight line, the larger the difference between the local integration degree of the region corresponding to the point and its global integration degree compared with the region corresponding to the scattered points in the vicinity of the fitted straight line. This indicates that there is a mismatch between the local integration and the global integration, and the local space structure is more different from the overall space structure, which in turn can be interpreted as a weaker self-similarity. Conversely, if the colored points are closer to the fitted straight line, the local integration degree of the area and its global integration degree are more consistent. The local space structure is not much different from the overall space structure; the higher the intelligibility, the stronger the self-similarity.

The intelligibility value of Xiaoliangjiang Village is 0.487, which is slightly lower than 0.5, and the intelligibility is relatively low, so people in the localized area of the settlement have a relatively low degree of perception of the whole of the settlement. The colored scatter points in the linear regression analysis of this settlement show a concentration in the middle and far away from the fitted straight line, with a small distribution on both sides. This indicates that people in most of the settlement spaces have a weak ability to perceive the whole locally, the local spatial structure is somewhat different from the overall spatial structure, and the self-similarity is not too high.

The reasons for the low intelligibility of the Xiaoliangjiang Village are considered to be the following:

• 1. In the 1970s, Xiaoliangjiang Village continued to expand to the peripheral areas, and many new buildings were built on the river bank area in the south and on the sloping land in the east. The proportion of new buildings is as high as 65%. The new buildings built by the villagers have destroyed the original traditional settlement style, and the traditional street network structure has been damaged. As a result, the localized space does not reflect the overall space well.

• 2. Xiaoliangjiang Village is located in a valley, and the layout of its internal streets and lanes changes with the terrain. Compared with the regular layout of settlements in plain areas, the layout of settlements in valleys appears intricate. The streets and lanes inside are free, changeable and complex, showing a natural state of self-organization. This also leads to a decrease in intelligibility.

• 3. There are many dead ends in the settlement, which results in some spaces not being well integrated into the entire space system, making it difficult for people to perceive the entire settlement space. At the same time, the existence of dead ends will interrupt people’s walking paths, reduce people’s sense of coherence and smoothness of the entire space, and make people feel lost or uneasy.

Application of results

Identify areas for expansion

Through the research on Xiaoliangjiang Village, it’s evident that the internal space of the old village area is relatively tight, with narrow roads and limited outdoor activity areas. A large number of buildings are built on the hillside, and the overall trend is to expand to the east. The terrain south of the highway is too steep and shaded to be suitable for residents. In the northern part of the new village, there is a road connecting to the northeast (Fig. 10). The north side of the road features a gentle slope, making it suitable for building houses and better connected to the old village, thus chosen as the expansion area.

Fig. 10

New planning area in the settlement

Newly built residential style

By analyzing the topology of the residential buildings in Xiaoliangjiang Village, the layout style of the new architectural courtyard is designed according to the iterative approach of its basic units, as shown in Table 2.

Table 2 Courtyard relationship diagram

Design new architectural courtyard forms according to different space requirements. The newly designed architectural courtyards are divided into four types, corresponding to the four topological structures. The courtyard enclosed on two sides corresponds to its basic unit layout. Iteratively more complex courtyard structures enclosed on three sides and four sides are generated based on its basic units. In this way, the newly designed architectural courtyard types continue the types found in the original settlement. At the same time this follows the same pattern of growth as the original architectural courtyards, that is, the generation of more complex courtyard forms by iterating over the basic types of courtyards.

Improvement of the road system

Iteration is one of the key concepts in fractal theory, which can explain and deduce the process and logic of settlement formation. By finding the basic shape of the settlement space, that is, extracting the “fractal elements”, and then performing similarity iterations on the “fractal elements” at different levels, a nested spatial form can be generated at different scales [43].

By calculating the number of fractal dimensions of each level in Xiaoliangjiang Village, it is found that the roads in Xiaoliangjiang Village have self-similar characteristics and have the conditions for extracting “fractal elements” and carrying out fractal iteration. Meanwhile, by analyzing the fractal dimension value of the settlement, it can be found that the fractal dimension value of the small-scale roads of the settlement is low. By increasing the coverage of some small-scale roads, the fractal dimension value of the small-scale roads of the settlement is improved. This will reduce the gap between the intra-cluster roads and inter-cluster roads fractal dimension values and improve the road network self-similarity.

Firstly, the fractal basic unit of the road in Xiaoliangjiang Village is extracted. The roads in Xiaoliangjiang Village are simplified to get simple axes. Then, select an area in the settlement to extract the fractal basic unit. Appropriate splitting of the roads in the region can get several “T”-shaped roads. The “T”-shape is the smallest unit for the fractal iteration (Fig. 11).

Fig. 11

Process of extracting fractal elements

In the software, VB6 establishes a coordinate system and mathematical functions for programming to create the “T”-shaped iteration system to get the program that can be controlled by the corresponding parameters (random iteration size, rotation angle). The following results are obtained after 10 or 15 iterations of the “T-shape (Fig. 12).

Fig. 12

Results of 10 or 15 iterations

Subsequently, the fractal graphic initially obtained after iteration is combined with the original settlement expansion area, and the placement needs to take into account the road scale and the topography of the expansion area (Fig. 13). It can be found that because the generated fractal graphics are too rigid and have a large gap with the original road structure of traditional settlements, the generated graphics need to be optimized. The optimized graphics are similar in scale to the road structure of the original settlement, and also conform to the topography of the expansion area (Fig. 14). Finally, the lines are converted into roads with width to get the new planned road network (Fig. 15). The distribution of roads in the planned settlement is shown in Fig. 16.

Fig. 13

Iteration results combined with original settlement

Fig. 14

Optimize the results of the iteration

Fig. 15

Roads in the expansion area

Fig. 16

Road map of the settlement

According to this planning, the planning results are verified by counting the intelligibility of the space syntax and box-counting method, and the data comparison before and after planning is shown in Table 3. The fractal dimension value of the road after planning is shown in Fig. 17. The overall fractal dimension value of the road is 1.531, which is higher than 1.499 before planning. The fractal dimension value of the 12.5–25 m scale is 1.292; The fractal dimension value of the 25–50 m scale is 1.611; The fractal dimension value of the 50–100 m scale is 1.665. The fractal dimensions at small scales are somewhat increased compared to the pre-expansion period, and the similarity between the 12.5 m and 25 m levels is improved. The fractal dimension values of several other levels have also increased.

Table 3 Comparison of data before and after planning

Fig. 17

Results of road fractal dimension values after settlement planning

The value of intelligibility after planning is shown in Fig. 18. The value of intelligibility after planning is 0.250, and the intelligibility is much lower than the previous value of 0.487. The local space has insufficient ability to perceive the whole, and the difference between the local space and the whole becomes larger.

Fig. 18

The intelligibility of the planned settlement

Improvement of settlement space

By calculating the fractal dimension values of each level in Xiaoliangjiang Village, we understand that the fractal dimension values are higher in the scale of 12.5–25 m. The dimension values in this scale can be appropriately lowered in the updating plan. Simultaneously, by increasing the fractal dimension values of the other two levels, the continuity of the fractal dimension values of each level will be better, and the self-similarity of the settlement will be improved. In this way, the settlement space can be closer to the “bottom-up” self-organized growth model.

There are several vacant buildings in Xiaoliangjiang Village, some of which are old and in poor condition. The street space is more complex. At the same time, more and more villagers are moving out from the center of the settlement due to the growing demand for better living standards, resulting in a lack of vitality within the settlement. In order to enhance the vitality and viability of the settlement and slow down the process of its decline, some of the more dilapidated buildings with little preservation value can be systematically demolished in the planning and protection of the settlement. In this way, the demolished areas can be used to build outdoor squares for villagers’ activities, providing villagers with more leisure and recreation places. At the same time, the construction of some small-scaled squares can reduce the fractal dimension value at this scale so that the difference between the fractal dimension value of the large scale and the small scale can be reduced, and the self-similarity of the settlement can be improved.

The location of the outdoor squares are shown on the map (Fig. 19). The south side of location ① is the Xiaoliangjiang Cultural Activity Center, and there is an ancient tree on the north side. The wide canopy of the old tree can form a semi-outdoor space. Constructing a small square at position ① can connect the cultural activity center and the ancient tree area, forming an indoor-outdoor-semi-outdoor composite space. The buildings in ②, ③, and ④ are too dilapidated and have little preservation value, so converting them into an outdoor activity area can effectively improve the quality of life of the neighboring residents.

Fig. 19

Settlement planning scheme map

Combining the previous road network generated in the planning area, the layout pattern of the building compounds generated in the previous iteration, and the new road network generated in the iteration are combined to build a completely new area together. The building compounds in the new area are arranged along the side of the planned road, and an area is reserved for outdoor activities for the sake of the residents’ recreational activities (location ⑤ in Fig. 19).

According to this planning design, the planning results were validated using the box-counting method. The fractal dimension values of the settlement after planning are shown in Fig. 20. The data comparison before and after planning is shown in Table 4. The overall fractal dimension value of the settlement is 1.651, which is roughly the same as the fractal dimension value before planning. The fractal dimension value at the 12.5–25 m scale level is 1.712, which is lower than the 1.719 before planning. The fractal dimension value at the 25–50 m scale level is 1.680. The fractal dimension value at the 50–100 m scale level is 1.553. The fractal dimension values of these two levels have increased compared with before planning.

Fig. 20

Result of the calculation of the space fractal dimension values of the settlement after planning

Table 4 Comparison of data before and after planting

Discussion

Characterization of pointwise self-similarity of settlement

Using the topology theory, the courtyards in Xiaoliangjiang Village are transformed into topological relationship diagrams. According to the topological relationship diagram, the internal logical relationship and the positional relationship between the buildings in the courtyard can be found more clearly, and the pattern of building arrangement can be visualized so as to find out the basic unit and its iterative way.

This iterative generation based on the basic unit structure allows for similarities between different courtyard layouts in the settlement, both locally and as a whole. Although each courtyard layout has its own unique points, they can all be traced back to the same basic unit structure, which is varied and expanded in a symmetrical manner. This similarity creates a sense of unity and coherence throughout the settlement while giving each courtyard a certain uniqueness.

The natural environment is one of the important factors influencing the formation pattern of settlement architectural courtyards. Natural factors such as geography, climate conditions, and water resources affect the site selection, architectural style, and courtyard layout of the settlement. In the Xiaoliangjiang Village area, the settlement buildings basically reflect the traditional Feng Shui pattern. The overall trend of the buildings follows the contours of the slope, rather than completely facing south like a plain settlement. In order to conform to the terrain, some courtyards have an outer outline that is not absolutely rectangular, but some changes are added to the shape of the courtyard to adapt to the terrain where it is located. The layout of the settlement buildings is based on the mountain, and is scattered layer by layer, as if growing naturally on the mountain. It is a “bottom-up” generation model.

The courtyard space structure of Xiaoliangjiang Village has the characteristics of traditional Shanxi and Hebei residents’ living. There are several types of housing construction: main room, wing room, side room and gatehouse. It is a typical traditional courtyard model. The layout of each room is also influenced by Shanxi and Hebei culture. Each room has a clear layout position and hierarchy.

In Xiaoliangjiang Village, the form of courtyards generally reflects the economic status of the owners. Families with higher economic status usually own more houses, which corresponds to the form of courtyards enclosed on four sides in settlements. Some families also want to obtain more building space, so they add two floors to meet the living needs of family members. At the same time, such a courtyard has a stronger sense of enclosure and provides more space and privacy. However, the construction and maintenance of these houses require considerable financial investment.

Characterization of the linear self-similarity of settlement

By fractal measurement of the roads in Xiaoliangjiang Village, it is found that the road network in Xiaoliangjiang Village has a certain degree of self-similarity. Comparing the fractal dimension values of different scale levels, it can be seen that there are some differences in the road structure of different scale levels. From the large-scale level to the small-scale level, the fractal dimension values show a trend from high to low. It shows that the three levels of entrance roads, intra-cluster roads, and inter-cluster roads present a gradual increase in self-similarity. It also reflects that the road coverage of the larger level is higher, and the accessibility of the roads is better. From the small-scale perspective of Xiaoliangjiang Village, we can see many lanes that are not connected, making it difficult to form an interoperable mesh structure, which affects the integrity of the spatial form of the settlement and reduces the self-similarity.

After planning, the fractal dimension at small scales has increased to a certain extent compared with before expansion. The fractal dimension values of other levels have also increased, and the similarity between each level has increased to varying degrees. It can be seen that the road network generated through the fractal iteration of the basic “fractal elements” is in line with the self-growth pattern of traditional settlements, and the original road network structure of the settlement has been continued in the expansion area and the road structure has not been damaged.

The layout of streets and lanes within Xiaoliangjiang Village shows a natural state of self-organization. This means that the natural environment has a profound impact on the layout of settlements. The direction, width, and curvature of streets and lanes are all affected by the topography, forming a layout pattern that is integrated with nature. This naturally formed layout reflects the harmonious and symbiotic relationship between humans and nature, as well as the characteristics of regional culture and historical heritage.

In addition, the road pattern in Xiaoliangjiang Village is also affected by clan concepts. The settlement roads take the ancestral hall and temple area in the center of the settlement as the center and radiate to the surrounding areas, forming a cross-shaped main road. The main road in the east–west direction runs through the old village area, forming a quick passage connecting the east and west areas of the settlement. The main road heading south leads directly to the main entrance and exit of the settlement and is the only way for most villagers to enter the settlement. The northbound main road is divided into two secondary main roads, namely “East Street” and “West Street”. The important buildings in the settlement are arranged in sequence along the north–south main road, forming an axis. Branch roads extend from both sides of the north–south main road and gradually cover the entire settlement to form a road network.

Characterization of faceted self-similarity of settlement

By measuring the fractal dimension of the settlement space of Xiaoliangjiang Village and comparing the fractal dimension values of different levels, we find that the spatial form of different scale levels does not differ much, which reflects a certain self-similarity of the settlement space of Xiaoliangjiang Village. Among them, the fractal dimension value of the small-scale hierarchy of settlements is higher. The first reason is, because of the limitation of mountainous terrain, the construction area is restricted to a certain range, resulting in a compressed construction space. The second reasons is, in order to satisfy the ever-increasing demand for material space, local residents have carried out a large number of self-organized construction activities. After a long period of superimposed construction, the settlement has formed a highly compact spatial form. The differences between the levels are due to the intervention of the influencing factors in the external environment. For the similarity of the spatial form of the settlement, the difference in the fractal dimension value is within a reasonable range, which further verifies that there is a good self-similarity between the whole and the local in the space of Xiaoliangjiang Village. The space combination of small-scale residential compounds constitutes the street space of the settlement, and the space combination of different streets constitutes the whole of the settlement space. The interactions and influences of spaces of different scales constitute the space whole of the traditional settlement with self-similarity.

After planning, the fractal dimension value at the 12.5–25 m scale level is lower than before planning. We believe that the reason is that some small-scale buildings were demolished, which resulted in a decrease in the fractal dimension value of this scale. The fractal dimension values at the 25–50 m scale level and the 50–100 m scale level have increased compared with before planning. We believe that the reason is that the size range of the expansion area covers these two scale levels. After planning, the fractal dimension values between each level are more similar than before planning, indicating that the self-similarity of settlements has been improved. The original settlement space texture has been continued in the new area, and the settlement planning follows the self-organized growth principle of traditional settlements.

The results of measuring the space intelligibility of the settlement in Xiaoliangjiang Village show that the intelligibility of Xiaoliangjiang Village is low. It reflects that most of the localized spaces in the settlement have a weaker ability to perceive the overall space, and it is more difficult to recognize the space. It also indicates that there is a large difference between the localization and the whole of the settlement. The self-similarity is low. The intelligibility after planning is lower than before planning. We believe that there are two reasons for the decrease in intelligibility: firstly, the road network was made very complex at the beginning of the traditional settlement to resist the invasion of foreign enemies, and the road network of the newly built area continues the complex structure of the original settlement’s road network, resulting in a decrease in the degree of perception of local space to the whole space after the expansion. Secondly, the expansion area is far from the core of the settlement, the newly planned road network is a bit dense, and the expansion area creates a new group, which has an impact on intelligibility.

The Xiaoliangjiang Village, after planning, shows opposite results in terms of self-similarity in terms of intelligibility and box-counting method, and we believe that there are two reasons for this. One is that in the fractal theory there is the concept of basic type. The basic type generates nested patterns of spatial form at different scale levels after many iterations, and each scale level contains the nature and information of the whole space system. Moreover, the self-similarity of fractals can be used to generalize not only the similarity between the local and the whole but also the similarity between the local and the local. These are not available in the concept of intelligibility, so intelligibility cannot be used to describe self-similarity. The second is that settlements cannot be too regular due to the need for self-defense. If outsiders are able to speculate the whole picture through the localization, this is not good for the security of the settlement. Therefore, too much intelligibility is contrary to the security needs of the settlement. Self-similarity is necessary because it allows the entire organization to have an inherent constitutive regularity in spite of the overall irregularity or messiness. This is the fundamental reason why settlement can exist and grow because completely irregular objective things do not exist in nature. This compositional mechanism, which develops by inherent growth laws and creates diversity outside, is not only the compositional law of settlements but also the compositional law of all things in nature. From this, it is judged that it is more reasonable to use fractal theory to explore self-similarity.

Conclusion

This article takes the national traditional settlement Xiaoliangjiang Village as an example and analyzes the self-similarity of Xiaoliangjiang Village with the help of Matlab and DepthMap space analysis software, taking topology theory, fractal theory, and space syntax as the theoretical basis. At the same time, it is analyzed comprehensively from three perspectives: building, street, and local space. Topology theory is used to study the self-similarity of buildings, fractal theory is used to study the self-similarity of roads in the settlement, and fractal theory and space syntax theory are used to study the self-similarity of local spaces in the settlement. Combining multiple theories and methods to investigate the relationship between the local and the whole in the settlement, the investigation of the self-similarity of the settlement is more complete. The main conclusions of the study are as follows:

(1) The architectural courtyards of the settlement are iterated with the “L”-shape as the basic structural unit, which generates a variety of courtyard layouts in the settlement. (2) The road network of Xiaoliangjiang Village has self-similarity. When expanding Xiaoliangjiang Village, the “T”-character can be used as the basic type to iterate and generate new roads, and it continues the road structure of the original settlement, which is a guide for the expansion of the settlement. (3) Comparing the fractal dimension values of different levels, Xiaoliangjiang Village presents gradually increasing self-similarity from the three levels of entrance roads, intra-cluster roads, and inter-cluster roads. The roads of the settlement at the small scale did not form a mesh structure, and the road structure was incomplete. (4) The space morphology of different levels in the settlement does not differ much, and the settlement space has a certain degree of self-similarity. The spontaneity and self-organization of settlement construction make the spatial forms complex and diverse and the fractal characteristics obvious. (5) Intelligibility cannot be used to describe the self-similarity of settlements, although it can be used to analyze the relationship between the local space and the whole.

In order to preserve the characteristics and appearance of traditional settlements, as well as to respect the layout and structure of traditional settlements, it is necessary to carry out original-intent planning and expansion of traditional settlements. This mode of planning and expansion aims to protect the uniqueness of the settlement, maintain its original historical and cultural values, and integrate with the surrounding environment. Through the study of the self-similarity of the settlement, the existing structural and layout characteristics within the traditional settlement can be found. These features are analyzed to obtain the basic type, which is then deduced and expanded to form a new settlement plan, and the new plan formed in this way has a certain degree of self-similarity with the original plan in both macro and micro.